The Mathematics of Ludo – Rules, Probabilities and Strategy

Parcheesi or Ludo is a more complicated game than it seems, and in this article I’m going to show you how the probabilities can help you improve your strategy so you don’t depend exclusively on luck.

Welcome then to the mathematics of Ludo.

1.Ludo Rules
2.The advantage in Ludo
2.1.Manage the advantage
3.Priority
4.Ludo Probabilities
4.1.Probability of Eating/be eaten
4.2.Probability to Save us
4.3.Probability in the Attack
5.Online Ludo
6.Practical Ludo Tutorial

1.Ludo Rules

Ludo is a board game of up to 4 players, where we can play 1 against 1, in pairs, or 4 individually. It can be played with 1 die in the classic version, although normally 2 dice are used to speed up the games.

• Each player has 4 chips to move them in their turn with the result of the roll of the dice, moving the desired checker with each die.
• The objective is to reach the goal with all the chips before the opponent, turning around with all of them until the entry of our color, introducing them in the goal with the exact value. And if the game is by pairs, they will have to be all the pieces of the pair.
• Before reaching the finish line with each tile, the player can eat the opponent’s chips that are not safe, build bridges or barriers with two tiles or put their chips safe in the safe boxes. These locks are distributed every 5 or 7 boxes.
• The rules for leaving the house are to roll a 5 with one of the dice or with the sum of the two.
• If you roll a double with both dice, you roll again, and if you roll a double 3 times in a row, your chip goes home as long as it is not already in the goal zone. There are other rules for different modalities but these are the official ones.

Our task then is to manage the movement of the chips in order to have the best chances of winning the game.

I am a specialist in 1-on-1 Ludo, and I will focus on this modality, but most of the theory I will teach is easily applicable in pairs or 4 individual.

2.The advantage in Ludo

As you have seen The rules are very simple, but before we know how to beat our opponent, how do we know who is winning?

Knowing which player has the advantage in Ludo is important and to find out this we will first analyze the board.

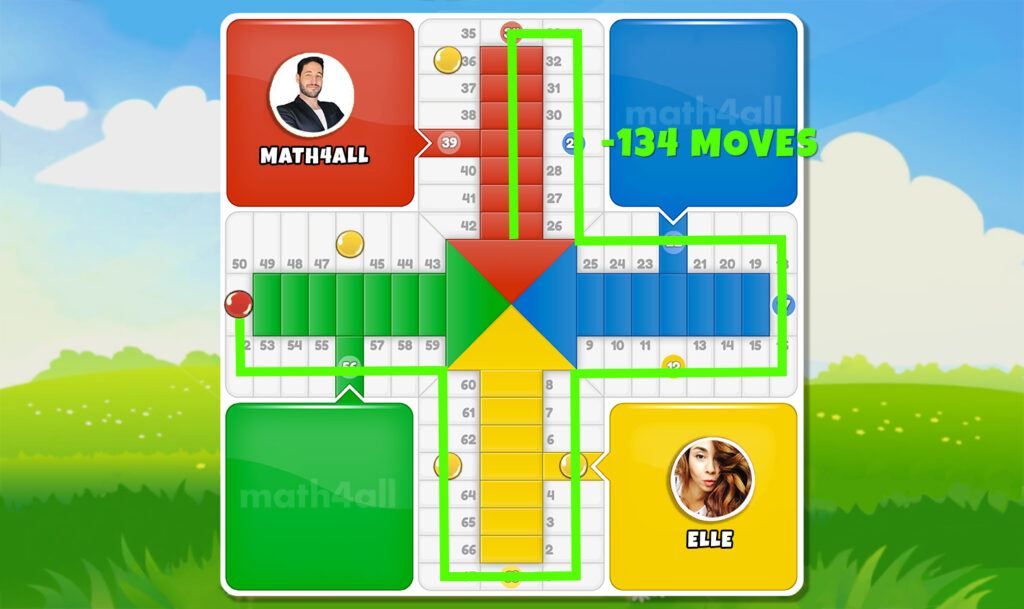
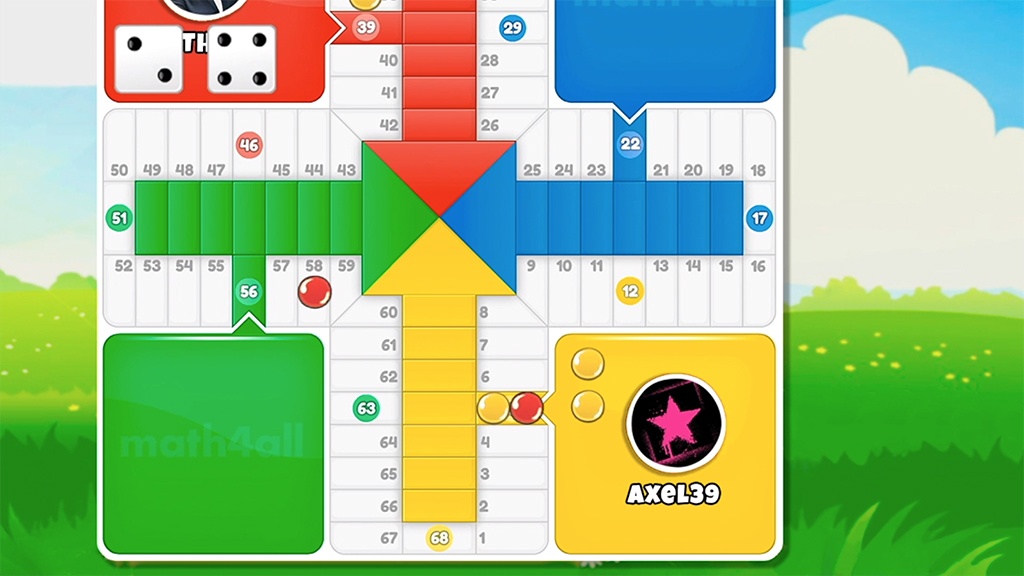
In Ludo, each piece goes through exactly 71 boxes from the moment it leaves the house until it enters the goal. If we multiply that by each checker we need a total of 284 moves between the 4 checkers to finish our game.

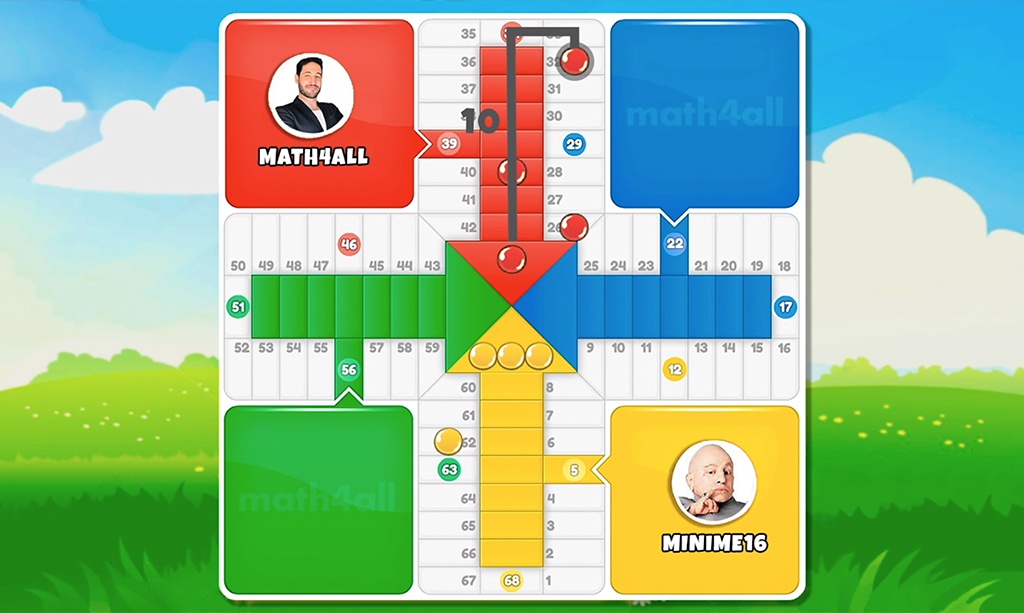
Suppose you have your tiles distributed with this configuration:

In this one, the chip closest to the goal needs 8 moves to enter the goal, the next closest 25 moves, the next closest 42 moves, and the furthest 59 moves. That is to say that between all of them they add up to 134 movements to finish our game or what is the same as saying that you have made 150 movements of 284 (it’s simply to make the subtraction).

If at the same moment your opponent has 130 moves, you know for sure that a priori you have more probability of winning the game, because you have less moves left to finish. It’s simple, isn’t it?

We have an a priori way of knowing who has the advantage, and although the advantage is not exactly the probabilities of winning as we will see, but it gives us an idea of how we are doing.

If you are able to see who has this advantage even if it is in a visual way, you have a very valuable information to control the game. Can you imagine what for?

The Ludo strategy is very simple, when you have an advantage you have to keep it, and if you lose it you have to recover it, that’s why it’s important to know if you are really winning or losing, to know if there is an aggressive or more conservative strategy to be applied. And this depends on the risk!

2.1.Manage the advantage

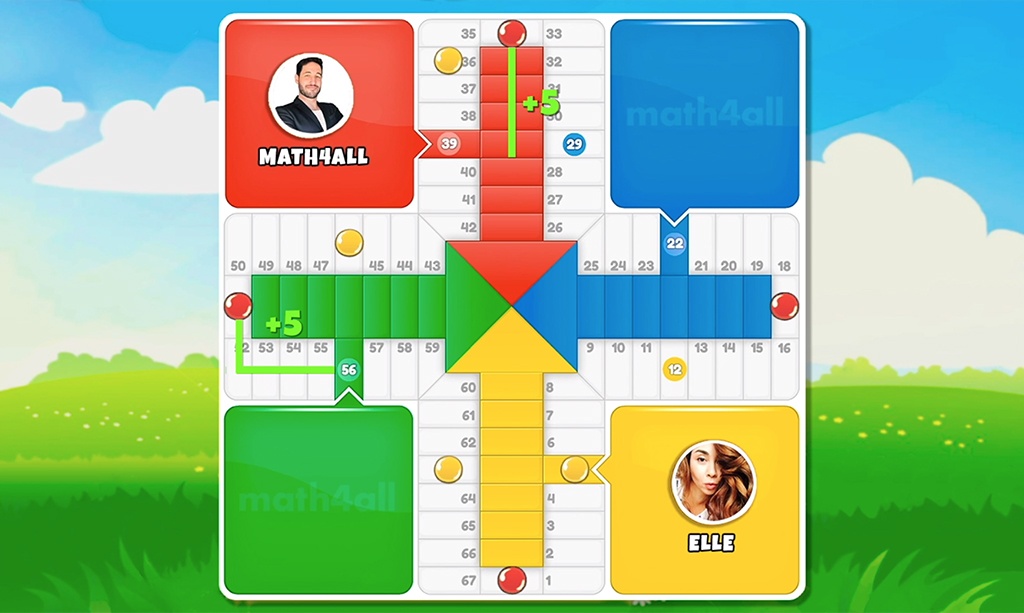
Imagine that you already have a big advantage and your opponent has all his chips on the left side of the board. In addition, you have a lagging chip that acts as a plug for his more advanced pieces. A common technique when your opponent sees that you have an advantage is to catch our chip with a bridge by bringing two chips closer together to catch it. But if you are aware of your ample advantage, you will see that it makes little sense to block their passage if for that we need to risk a checker. So the most intelligent thing is to move it to the other part of the board as soon as possible where it is safe, to continue with the same advantage but this time without risk.

Imagine another situation where you have enough of an advantage and can choose to move the most advanced chip by priority or the chip that is unsafe to put to safety. If you analyze and see that your advantage is enough to win, what is the point of leaving a chip at risk despite being a considerable distance away?

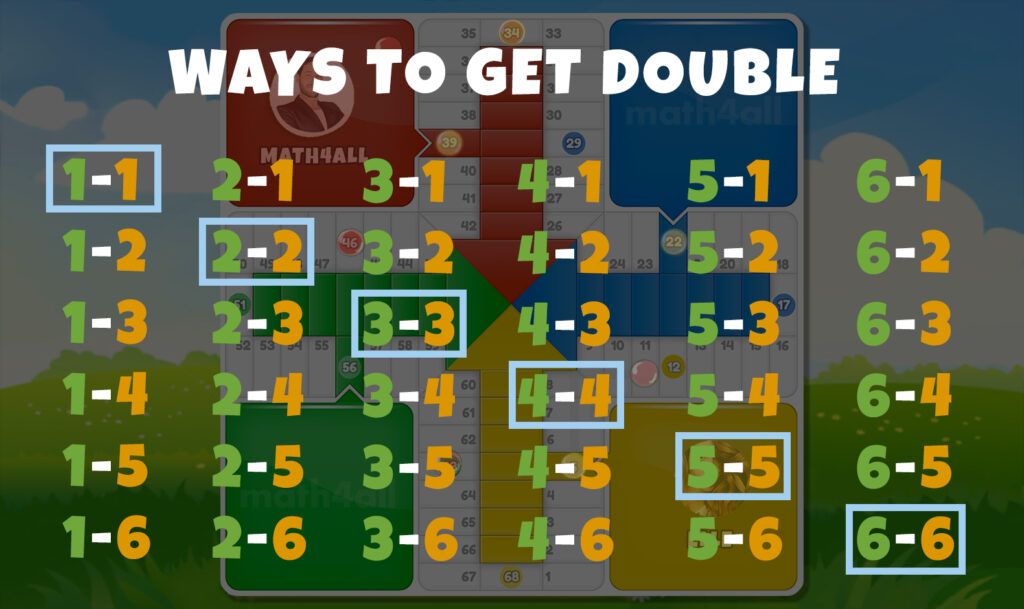
If your opponent rolls a double, he can bring the chip closer to yours and even kill it on the next roll, but what is the probability of rolling a double?

Drawing a double is probably easier than you think, since with 6 cases out of 36 we have approximately a 16.6% chance of getting it, or 1 sixth, that is to say that 1 out of every 6 times we make this decision we would be risking a game that we have practically won. This shows us the importance of having all the chips safe, especially in an advantageous situation. Any miscalculated detail can put the entire game at risk. So if you have an advantage, don’t risk it if it’s not necessary.

Another risk situation to avoid is to secure our chip in the opponent’s starting box when he has one chip at the start and another at home, or both at home. Because having a chip outside is worth a 5 to kill us and that will happen almost half of the times he throws (41.67%), which we are not interested in.

In conclusion, if you have an advantage big enough to win, you should take a conservative stance, that is, avoid risk or confrontation as much as possible by moving the necessary piece.

3.Priority in Ludo

As you have seen, there are situations where putting our chips in safety is more important than moving chips further ahead, so it doesn’t matter which chip we move?

I imagine that you think that if you move a backward or a forward chip you are moving the same chips in global computation, then choosing one or the other does not seem to give us more or less advantage.

But even if you don’t believe it, moving the most forward can give you more chances to win. Keep in mind that each goal adds up to 10, and if you always move the most advanced piece, you will arrive earlier with the same rolls, since you win that advantage earlier. Therefore, if you only have to reach the goal, always do it by priority and don’t move chips further back in a grouped way.

Moving all the chips in a group without a concept of priority is a mistake if it is not justified. Group movement involves moving the most backward chips and that moves your defense forward, allowing your opponent to move forward more easily and to pressure you with the advanced chips. Besides, when you move the chips in group, you advance very slowly with the chip in front of you and this does not allow you to reach the opponent quickly to press as soon as possible. In short, moving in a group does not make you lose the advantage as such, but it does have a strategic reason it takes away your possibilities of winning.

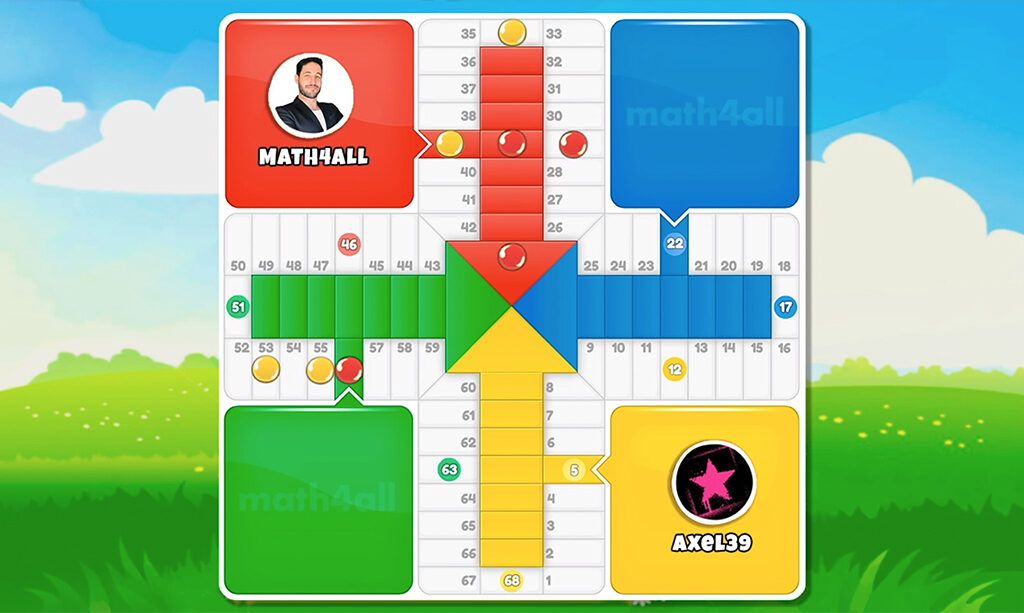
I guess you wonder if I am saying that the probability of winning and the advantage are not exactly the same, and indeed they are not.

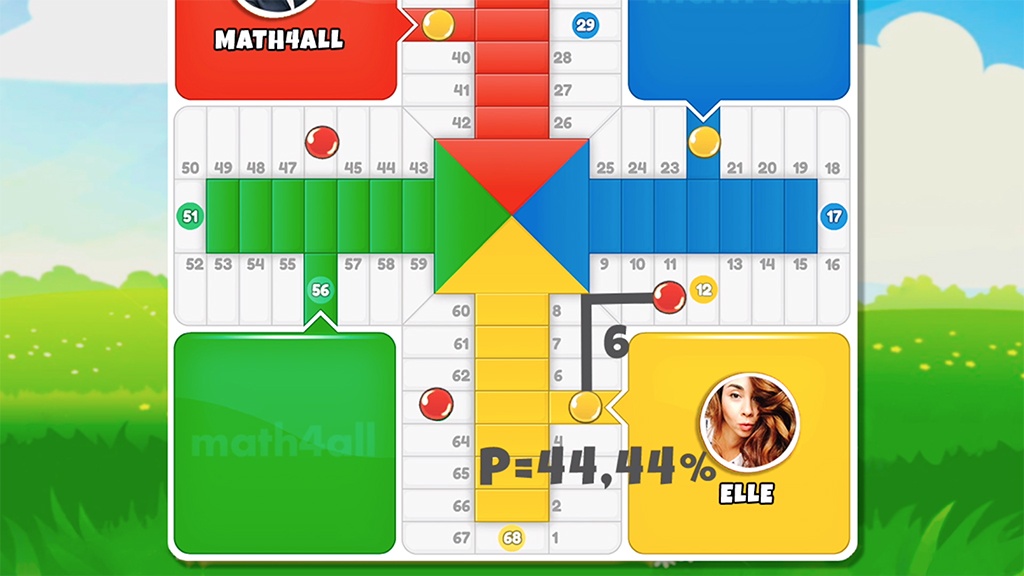
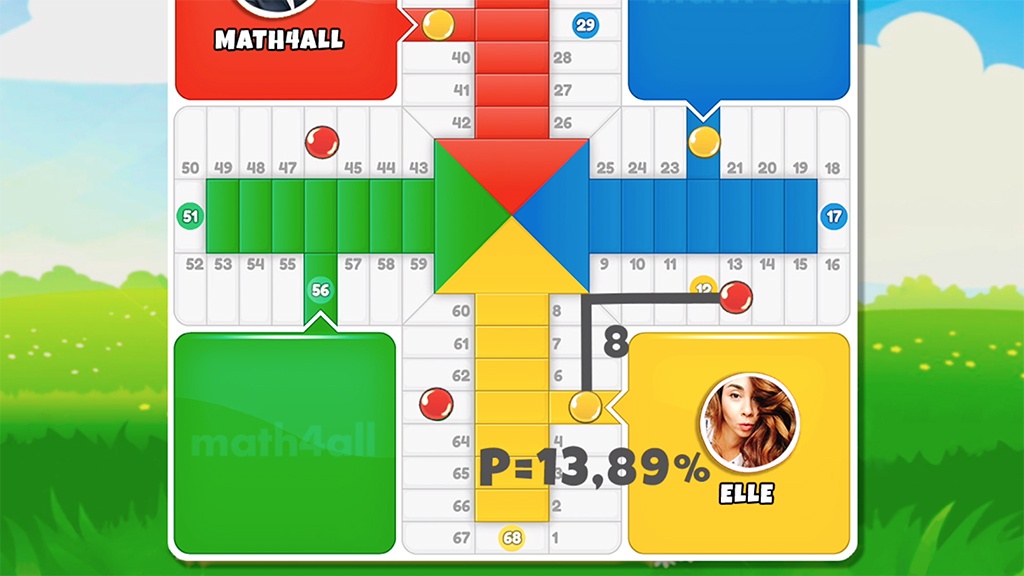
In this other example you can see that our opponent is further away in moves, however our probability of winning is lower. You wonder why? If you look at it, you still have to put in 4 chips and he is practically 1 throw away from being able to reach the goal with just one. You need at least 2 rolls to put in all 4 chips in, but if you don’t roll a 1, you still don’t have a choice because you still have 2 blocked chips.

Now you can understand that the probability of winning depends also on how we manage and position the chips apart from the advantage, and in this case it would have been better to put the chips further ahead in goal by priority before waiting so long.

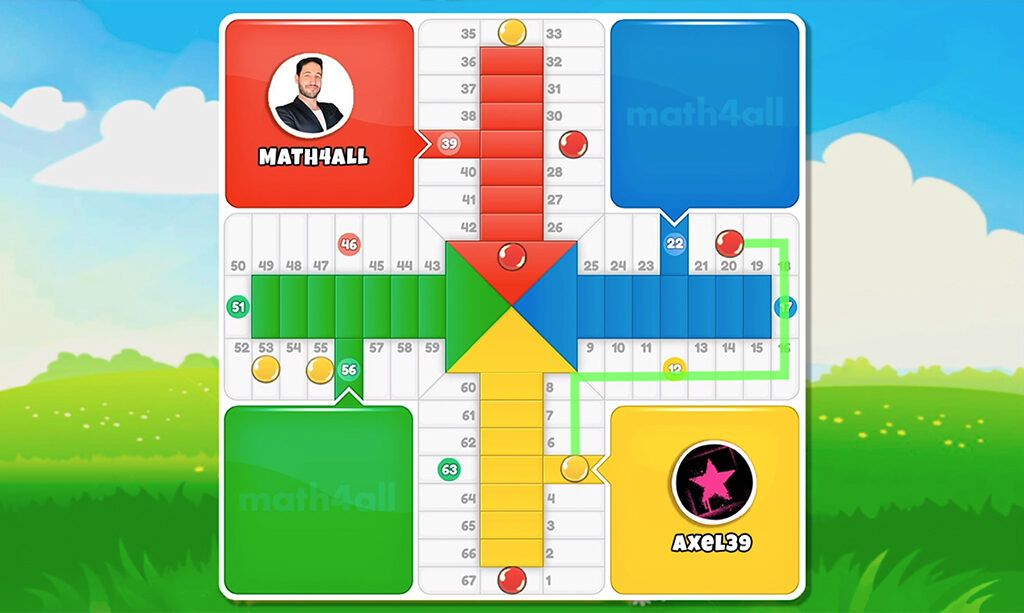
Another technique to avoid accumulating chips in the finish line is to leave your chips when they reach a distance of 10, because if you manage to put one chip in the finish line zone, the others will go immediately. You simply need 1 hit to place several chips, and that makes them less likely to pile up.

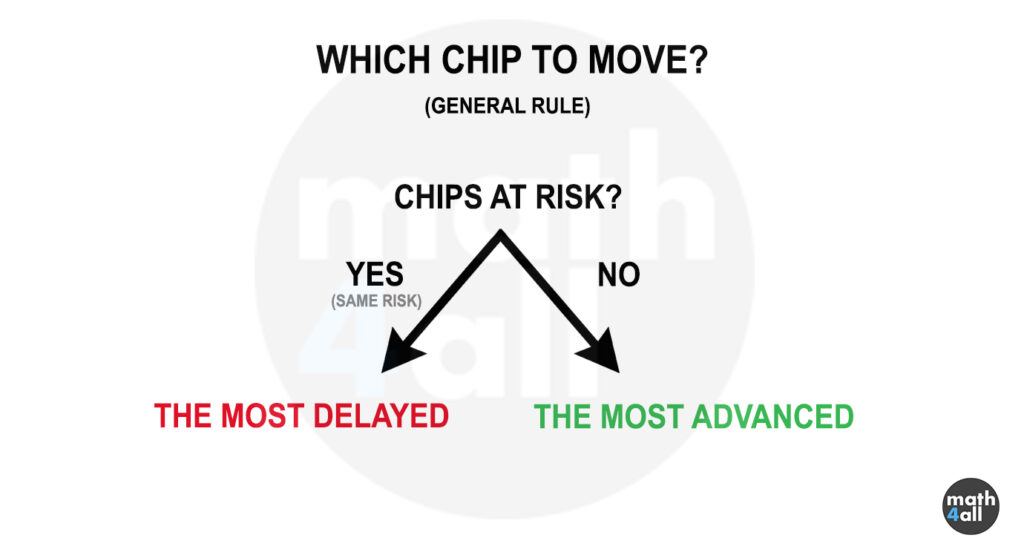
In short, when there is no risk, we always move the most advanced chip, but what happens when there is?

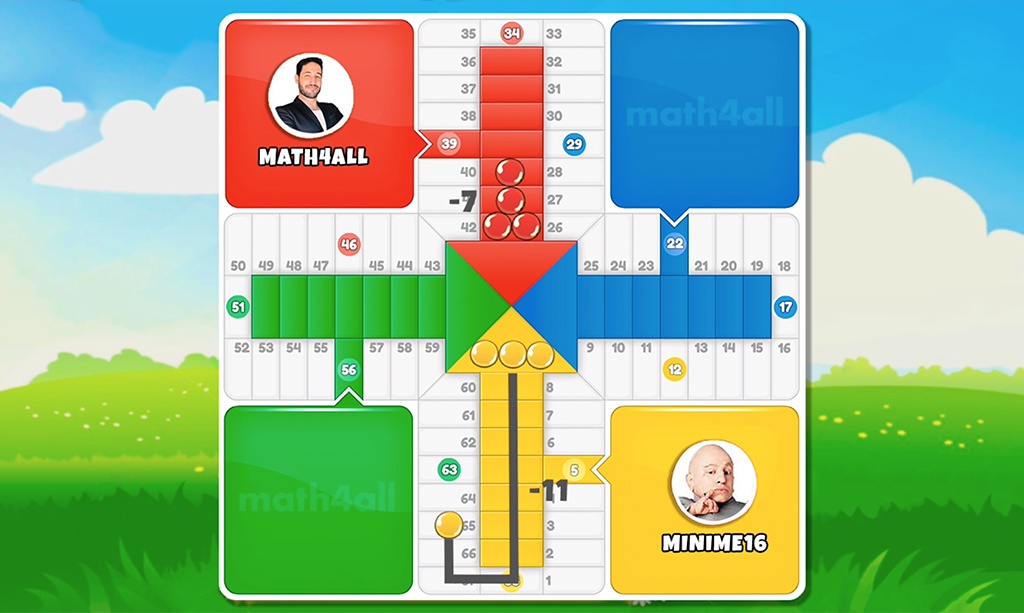
In this example we have already played 2 doubles in a row and we run the risk of roll a third one. If you do not have a chip to move in the goal zone that overrides the 3-double rule, you must choose which chip you put at risk in case the third double arrives. In this situation the decision that best minimizes the risk without taking into account the strategy is to move the most delayed chip, because in case of being eliminated it is the one that makes us lose less advantage. In this case we are choosing by priority the most delayed chip.

Although you may think that getting 3 doubles is complicated, and you are not wrong, in fact you have 0.46% chance of pulling 3 doubles before it happens, but when you have already pulled 2, getting a third one is exactly as easy as pulling the second one.

In short, the priority when there is risk works the other way around, and it is better to risk the most delayed chip whenever possible and strategically correct.

But if there is no risk, nor strategy, you will move and enter the goal with the most advanced chips, to avoid guys like minime to end up winning because you are absent-minded 😉

However, if your opponent is good, he will normally prevent you from doing this by forcing you to move the backward chips, so that he can move the front pieces to control the game. So be very careful!

4.Ludo Probabilities

You just saw how risk changes the priority to choose which chip to move, but how far should you move a tile so you don’t get killed? Is it better to be 2 boxes away, 4 or the same? What do you think?

–Out of shot

As you know the maximum value of a die is 6, and that makes the sum of two dice a maximum of 12. So I recommend you to be at a distance greater than 12 if possible, because more than 12 boxes can not kill you directly.

And what happens below 12, all distances are equally likely?

–On within range (distance less than 12)

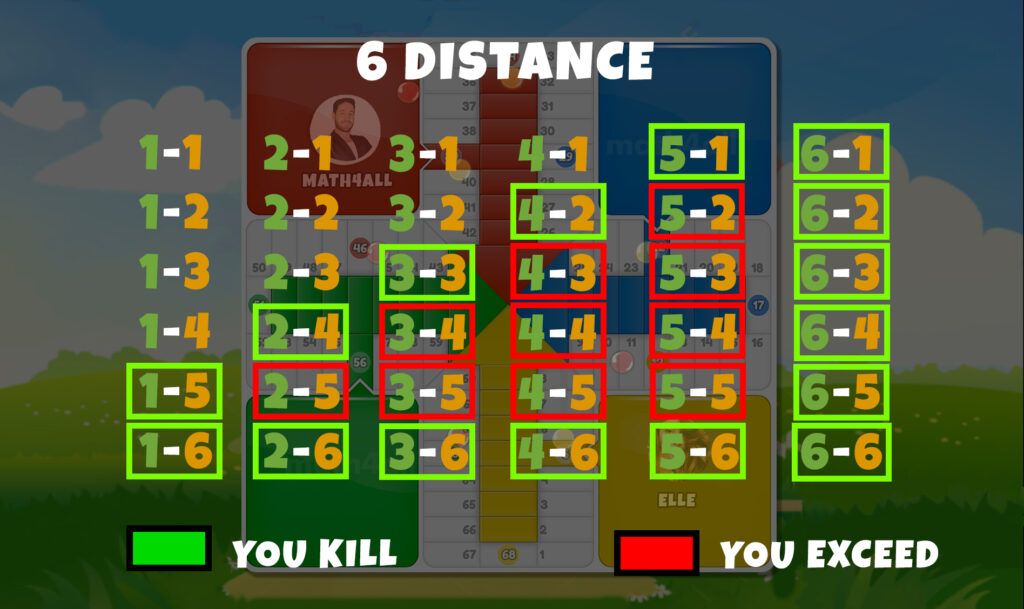
The truth is that it is not, because there are boxes that are within direct shot and others that are not. You’ll agree that at 6 boxes or less, either die can kill you, since a die reaches 6.

In contrast to more than 6 the opponent needs the sum of the two dice to kill you, which is more difficult by probability. Therefore it is also better to be 7 boxes or more away from each other whenever possible.

–On direct within range (distance less than 7)

And what happens to less than 7?

Even at a distance less than 7, the probability is not the same either, because besides killing you directly, it can do so with the sum and not all sums are equally probable.

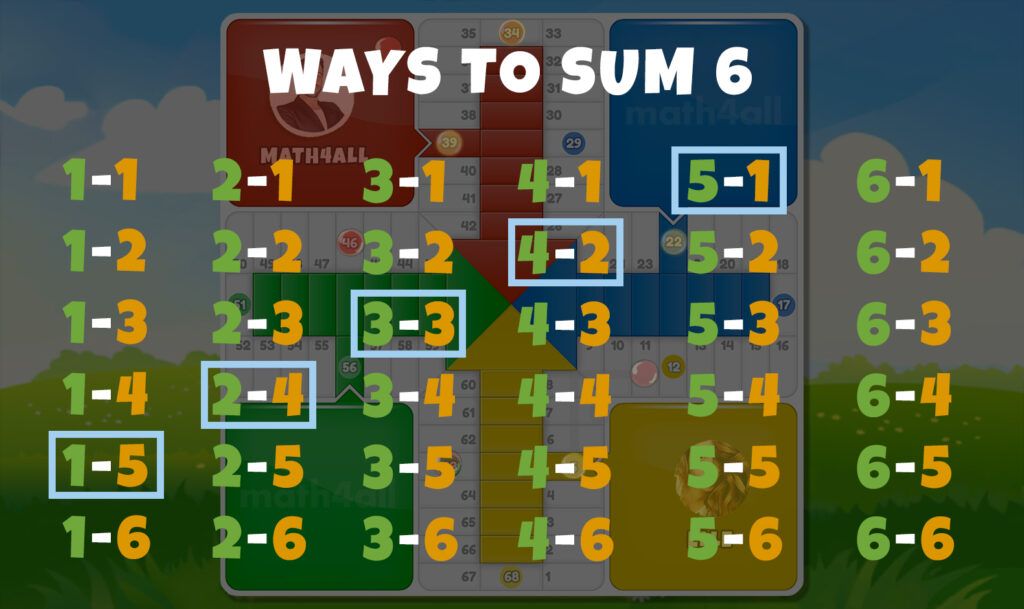
Do it directly if it has the same probability, because taking any value off the die is just as likely, it is the same to take a 3 as a 6. But do you think it is just as likely to add a 3 as a 6?

As you can deduce we can add 3 only in 2 different ways, 2-1 and 1-2, but we can add 6 in 4 different ways, so the probability of adding changes and in this case is higher for 6.

But how do we calculate all the probability?

4.1.Probability of Eating/be eaten

Knowing the probability of being killed both with the sum, as with the first die or the second one in a direct way is the probability of the union of the 3 events:

• A: “Let the value come out with dice 1“
• B: “Let the value come out with dice 2”
• C: “Let the value come out with the sum of dice 1 and 2”

We apply the probability for the union of 3 events::

P(AUBUC)=P(A)+P(B)+P(C)-P(A∩B)-P(A∩C)-P(B∩C)+P(A∩B∩C)

and this is simplified as P(A)+P(B)+P(C)-P(A∩B) because P(A∩C), P(B∩C) y P(A∩B∩C) are 0 since the sum of two dice can never give the same value as one of the two. (when talking about events A and B, A and C mutually exclusive)

But since I know that it doesn’t have to interest you, I’ll show you the results directly:

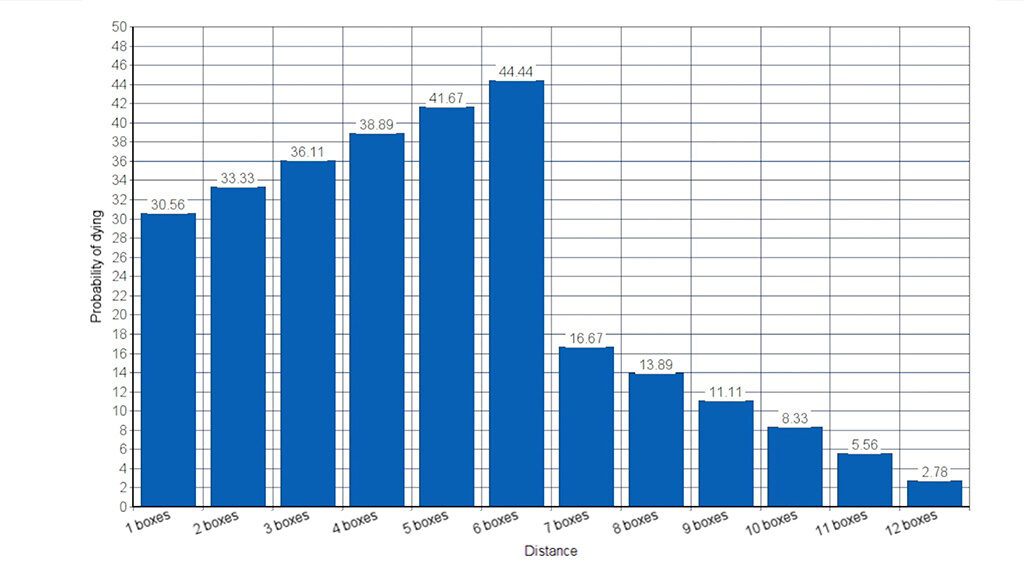
4.1.1.Probability regardless of the next die rollWhich can be represented by the following graph:

As you can see, being 6 boxes away is where you have the highest probability of being killed, thanks to the fact that, as you have already seen, it is easier to obtain with the sum, and the further you go from 6 the more difficult it becomes, as we deduced.

On the other hand, the closer you get to 1, the more difficult it is to be killed. This is the best distance at first, because if you think about it, 1 cannot be obtained as the sum of two dice. Was it what you imagined?

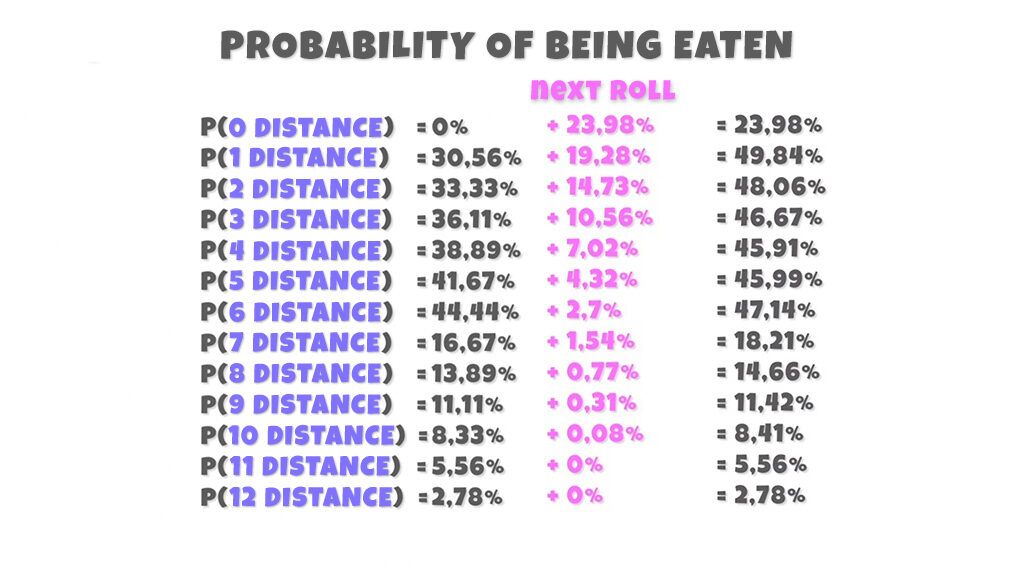
The problem is that at such a close distance there is more risk of staying within range on the next roll and this calculation is not taking it into account. For that reason we must also add the probability that the opponent has of killing us in the next roll if we are in that position.

4.1.2.Probability taking into account the next die roll

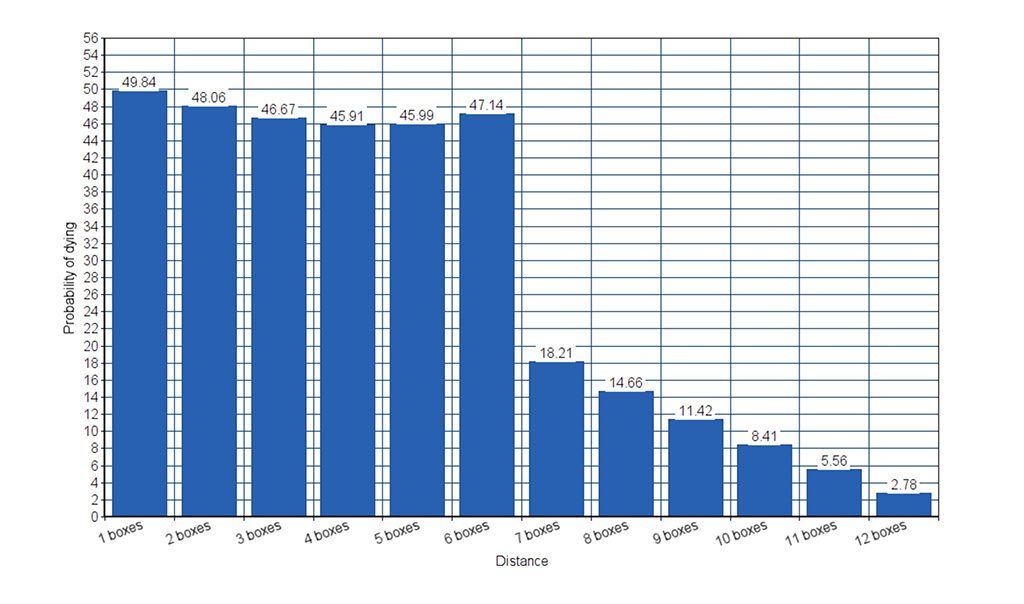
Updating also the graph:

And as you can see, things have changed a lot! The first positions have much more risk because of the next roll, and in the end the worst is the first position, because the probability of being killed in the next roll decompensates the balance of the other probability. And the best option is to put the chip at a distance of 4 or 5, which positions you further away and without as much probability of dying as at 6.

Did you never think that the Ludo could give for so much truth?

4.2.Probability to Save us

Now you know where it’s best to stand so you don’t get killed. But when you’re already far away, you have to think more about where to place your unprotected chip in order to reach an insurance with greater chances.

 

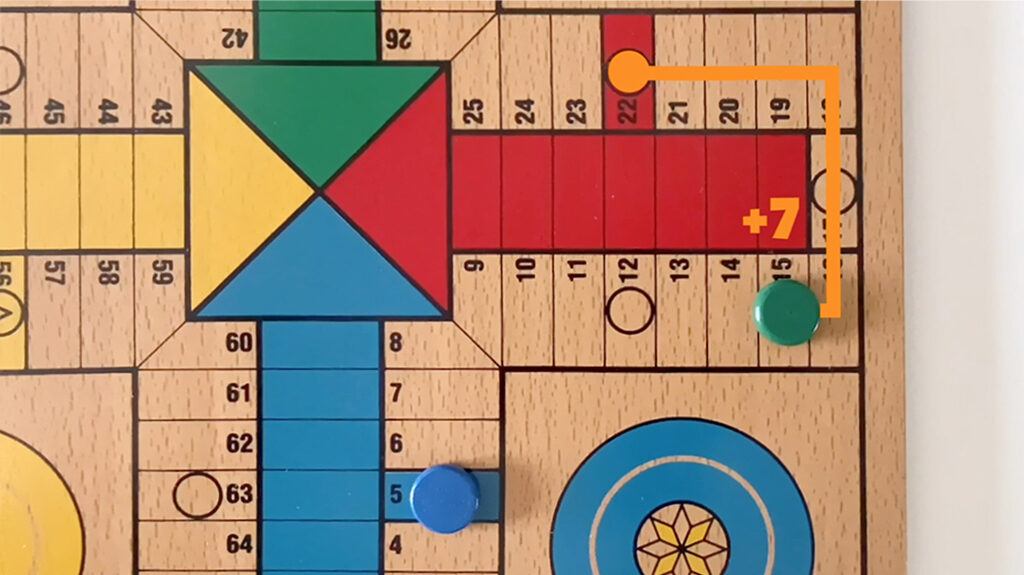
In this example we see that by placing the chip in box 15 you choose to save it with a 1 or by adding 7 with the two dice to get to 22, which is less likely. On the other hand, if you have the possibility of placing it in the box 16, you save the chip with a 1 and a 6, so you have a much greater chances of placing your chip in a safe box on the next roll.

and that’s because these zones are always better for getting you to safety.

4.3.Probability in the Attack

As you have seen, you can avoid unnecessary risks to avoid being eaten, but how do you manage an attack?

Thinking about attacking is using the same information from the table but this time in reverse, to position your chip behind, but this time looking for the highest probability and not the lowest. This is to place you from behind at 6 distance if you are going to repeat a turn or know that your opponent cannot move that piece. And in case you have the ability to escape then as close as possible, which is 1 if you are behind or 0 if you are in safety, because that is where you have more probability of eating him in the next roll if he decides to move it, as the table indicates.

But be careful not to run out of room for manoeuvre with the other chips, because being so close you run the risk of going over with the dice and being the one who ends up shooting, either with that checker or with the one you decide to move. So if that risk exists, the best according to mathematics is to be at a prudential distance of 6 boxes where you get an optimal benefit-risk ratio if your intention is to kill.

5.Online Ludo

In the next video you will be able to see the attack strategies that exist in Ludo, and how to manage the barriers, but in order not to make the wait too long you can try these strategies by playing Ludo online on different ludo games: Ludo Star, Ludo mundijuegos or Ludo Playspace.

Ludo Star

Pros: Very big community, it’s free.

Cons: Unobtrusive design, no turbo game. Few variants.

Ludo Mundijuegos

 

Pros: You can also play on the website, it’s free.

Cons: Need flash player for web, small community.

Ludo Playspace

¡play LUDO!
Pros: Puedes jugar en facebook, muchas modalidades, gran comunidad, gran personalización, es gratis.

Cons: Some customizations are chargeable.

I usually play playspace ludo because I like its design better, but above all because it allows to play turbo games, which is what I like, so I leave you a link in case you want to play it

I hope you find it practical and if you want more videos like this one of live play, leave a comment at the end of the article. Greetings.