The Mathematics of Blackjack

NOTICE: This article does not intend to promote gambling or ludopathy. It is an analysis focused on the mathematics of gambling, where it is explained whether gambling can be profitable or not and how to analyze it.

Do you think you can win at Blackjack? What is the best way to play? In this article we solve these and other questions with the help of mathematics.

1.Blackjack Rules
2.Blackjack Actions
3.Blackjack Payouts
4.Mathematical Study of Blackjack
 4.1.Chances of exceeding 21
 4.2.Chances of the Dealer exceeding 21
 4.3.Mathematical Advantage of the House
5.Basic Strategy
 5.1.Blackjack Chart 1 Deck
 5.2.Blackjack Chart Table Several Decks
6.Counting cards
7.Conclusions

1.Blackjack Rules

Blackjack is a French deck game for up to 7 players where the players face the house.

The goal is to get 21 with our cards or a higher value than the dealer, without exceeding the number.

If we exceed 21 or add a lower value than the dealer we’ll automatically lose our bet.

Once the bets are placed 2 visible cards are dealt to each player and only one for the dealer

Players must say based on their cards and the croupier’s if they want to hit, stand, double down, or split their hand

All cards are worth the numerical value they have, i.e. from 2 to 10, except for the figures that are worth 10, and the Ace that can be worth 1 or 11 to our interest

Payments are made on same time, and we can get 21 with more than two cards but will only be considered blackjack when done with two.

The house can only hit or stand, and only hits when its hand is below 17, so if it reaches or exceeds that value will stand automatically.

In case the dealer goes over 21 the players who are still at the table will win their bets and in case of a tie the player will regain his bet.

You can play blackjack with one or more decks being 6 decks the standard in the European Blackjack.

The American Blackjack has some different rules that allow you to modify if the dealer hits or how players can split their hands. In addition he deals himself a second card covered and you can consult it in case his first card give him the chance to do blackjack If effectively he gets 21, the players they’ll lose their bet before they even play. This speeds up the game and also decreases the house advantage.

2.Blackjack Actions

-Hit/Stand

In the first place, we can hit, while our sum does not exceed 21 depending on the card they give us we’ll be closer to 21, or instead we’ll lose the bet if we get over it.

-Double down

Para doblar nuestra apuesta necesitamos una mano que sume obligatoriamente 9, 10 u 11 y solo podrá hacerlo en el principio de turno. En caso de doblar tu apuesta solo podrás recibir una carta más.

To double down we need a hand which obligatorily sums 9, 10 or 11 and you can only do it at the beginning of the round. If you double your bet, you can only receive one more card

Unlike in American Blackjack we can double up with either hand.

-Split

If our cards have the same value, we can split each card into different hands to play them at the same time, but for that it is obligatory to add also a bet as the initial. You must also know that within a split hand, even if we sum 21 with the next card is not considered blackjack.

After splitting, most casinos allow to double the resulting new hands, and this gives us some advantage. (Not allowing it increases the house advantage by 0.12%).

-Insurance Betting

If the card uncovered by the dealer is an Ace, we can bet to insurance, if we feel that the house will get blackjack with the next card. If we’ve bet and finally gets it, we’ll be rewarded.

-Leave

And finally leave, which is only possible in the American Blackjack and if the player leaves  he will lose only half the bet.

3.Blackjack Payouts

–1 to 1 (one chip for each chip bet) if we beat the house.

–3 to 2 (three chips, for every two chips bet or one and haf for each chip bet) if we beat the dealer with Blackjack (as long as there is no tie). In the American Blackjack of Las Vegas you pay with 6 to 5.

–2 to 1 (two chips for each chip bet) if we win an insurance bet.

In the case of American Blackjack, it is also usual that if the player has blackjack and the croupier has a visible Ace, he is offered the possibility of charging blackjack with a 2 to 1 (instead of the usual 3 to 2) as an alternative to the insurance bet.

4.Mathematical Study of Blackjack

To analyze Blackjack at a mathematical level we must know that a French Deck has 52 cards.

– 4 of them are Ace,

-16 of them are 10 or Face card.

-The remaining 32 are numbers from 2 to 9

So we can draw some conclusions:

-Approximately one third of the cards, have the value 10 (which takes a fundamental weight).

-After that, there are only 4 cards that are Ace so if we want to get a blackjack we’re gonna need one of them but… which is the probability?

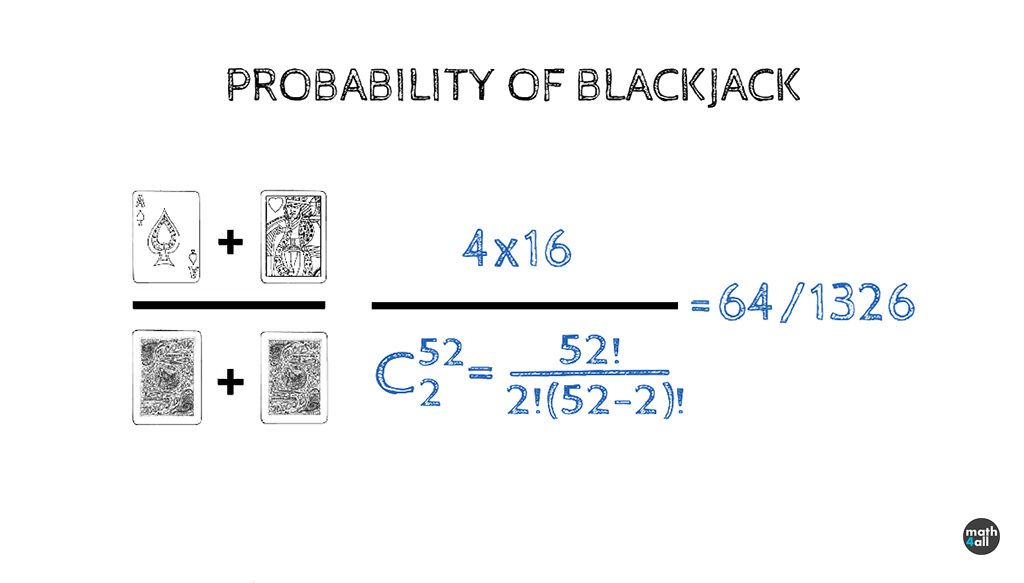
The probability of getting Blackjack are the ways we have to get 21 with 2 cards of all possible combinations to pull 2 cards out of the deck.

Or put another way, favorable cases between possible cases, which is not the same than odds, even are related.

To get 21 with 2 cards we need an Ace and a 10. And in the deck there are 4 Aces and 16 tens (between face cards and 10 value cards).

On the other hand, all combinations of 2 cards, combinations of 52 elements taken 2 at a time (where the order doesn’t matter, and they can’t be repeated),

so the final probability is:

4.16 / C52,2 which is equal to 64/1326 or a 4,8% chance of getting Blackjack (which was logical since we know that to have blackjack we always need an ace and there are only 4 in the deck).

In case of playing with several decks each figure or number maintains the same proportion, due to it’s the same 4 aces in 52 cards, than 8 in 104. But the probability of getting a particular result vary slightly, since it influences less to remove a card in a deck of 104 than in a deck of 52. So each game with different decks has its own probabilistic study.

4.1.Chances of exceeding 21

To calculate the probability of going over 21, we must to calculate the probability of going over for any hand and for that, we need to analyse hand in hand.

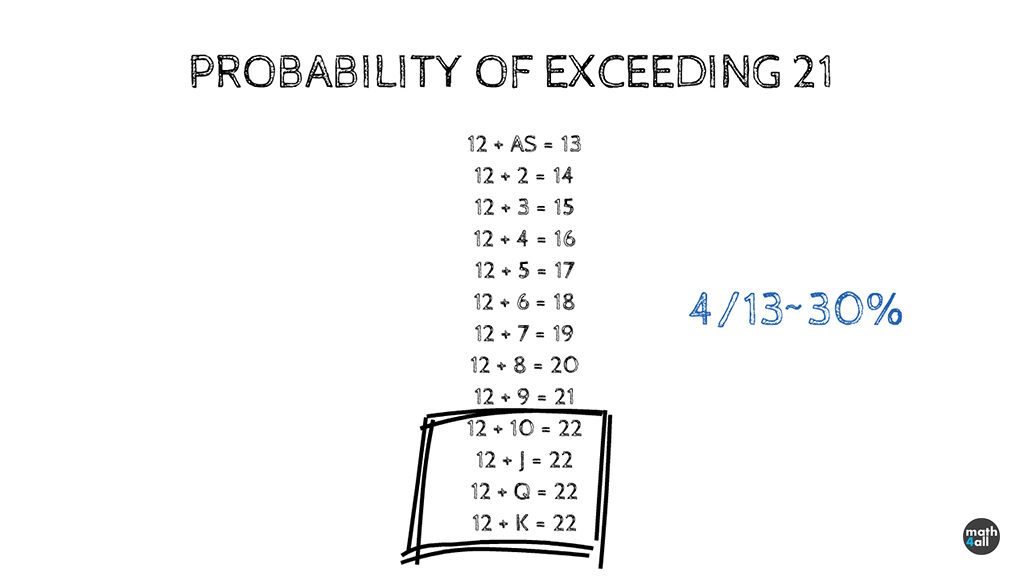
Let us imagine that our hand value sums for example 12 value:

When we hit, we are faced with all these cases:

As we see, initially there are 4 cases of 13 where we exceed 21. This is approximately a 30% chance, which means that with a 12 value only 30% of the time we hit, we will exceed 21.

(The calculation of this probability is a simplification because we really would have to take into account that the cards that make up the 12 vary slightly the probability of the card we have asked, but the difference with this calculation is not very large and also is much more complex to study and understand).

If we calculate the same for all possible hands and accurately we will obtain the following table:

As you can see, from 13, both us and the house we’ll exceed the most of the time.

Also note that if our sum is 11 or less we can never surpass 21 with one more card That’s why probability is 0.

4.2.Chances of the Dealer exceeding 21

As we just saw, if we don’t want to lose most of the time we must hit as long as our hand sum less than 14. The question is… If we put a limit on 14, do we have a chance of winning?

If we consider that the dealer always hits for a card until sum 17 or more, stand with a value less than 17 only makes you a winner when the dealer exceeds.

Or to put it another way, if the dealer doesn’t go over 21, his hand will always have a value equal to or greater than 17, so the players who stood with a hand less than 17 will lose their bet.

Well, according to the mathematical study carried out the chances that the dealer exceeds 21 depending on the card he has (and his strategy) are the following:

We see that for a high card the probability of go over is quite low being the Ace the card that offers the most advantages to the house.

For a low card the probability is higher, but note that in no case does it exceed 50%

If we average all of them we conclude that the dealer surpasses 21 in 28.35% of the times (368,67/13), which means that in the remaining 71.65% of the times you stand with less than 17 you’re gonna lose your bet.

House Limit

As we have just seen it’s useless to set a limit below the dealer limit, since we will lose in most cases.

But thanks to this we’ve discovered that the dealer’s up card offers us valuable information to make decisions.

After this we have the following questions:

-Why is the house limit 17?

-What if I copy the house strategy and I also stand from 17?

4.3.Mathematical Advantage of the House

If you realise the dealer always waits the player finishes his play before proceeding to play him. That means that if the player goes over 21, he loses his bet regardless of what the dealer does. So if the dealer also goes over 21 it is the player who loses anyway since he had been eliminated before. That makes the house wins in a case, which is really a tie and this happens 7.9% of the time you play. That’s about an 8% advantage over the player which is finally reduced to 5.6% if we consider that blackjacks are payed 3 to 2, instead of the equitable 2 to 1 .That’s the casino’s main advantage.

To fight this, the player has options that allow him to have a flexible strategy. He can double down when he’s interested, split hands, leave, etc. But most importantly, he knows a dealer’s card that will make him make those decisions (differents from hit or stand only) considering this card and this, is where math comes in once again.

5.Basic Strategy

In the 50s, a group of mathematicians led by Roger Baldwin developed the Basic Strategy. This is based on optimizing player decisions in such a way that the action he chooses it’s the optimal in terms of profit from among all the actions he can take. This bring us at first the maximum possible long-term gain.

And is achieved by developing a probabilistic model which calculates based on the player’s hand conditioned by the dealer’s card when it is more optimal to make the decision of stand, hit, double down, split or bet on insurance, either for hard hands that are inflexible as for soft hands (where there is an ace and can change the sum).

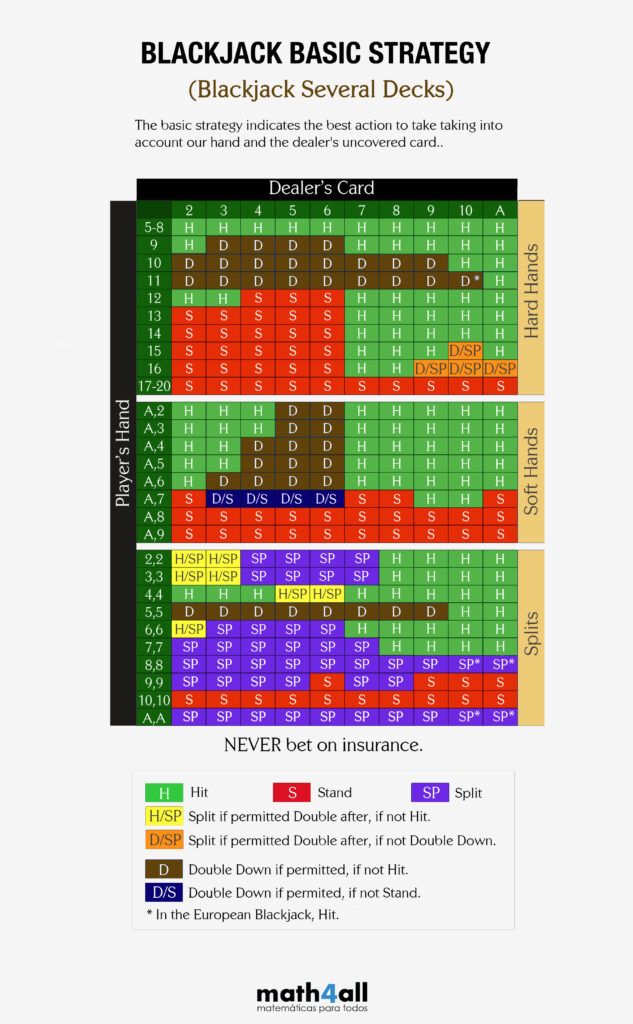
In the mathematical language we can say that by means of a recursive function with some defined final values, and a table with all the probabilities for the sum of the dealer, the maximum between the expected gain if he stands and the expected gain is calculated taking into account all the possible cards that it can receive when it asks for a card (the average of all the possible expected gains if it asks for the next card). With this a table of results is elaborated that assures us mathematically which is the most convenient action, making our strategy optimal whatever the combination of cards between the player and the dealer. So if you want to play Blackjack well I recommend you to download this blackjack chart:

DOWNLOAD BLACKJACK CHART 1 DECK

DOWNLOAD BLACKJACK CHART SEVERAL DECKS

As a detail, notice that in hard hands from 17, it gives us instructions to stand. That means that regardless of the card have the dealer, math tell us that the expected profit is always higher if we stand. That answers the question of why the house has 17 as a limit. if we understand that the house is also a player.

Look also, you should never bet on insurance. This is because although the dealer has an Ace mostly he won’t get blackjack.

Well, with this strategy we went from the previous 5.6% to a percentage of less than 1% for the bank that will vary depending on the rules of the table and the decks used (put table). We have to understand that even though it is an optimal strategy it doesn’t necessarily mean that it’s a winning strategy, since the balance of our advantage, despite being small, is still negative. And this is mainly due to the fact that the dealer’s high cards diminish our advantage more than the low cards, so even if we take the best decision, we will not necessarily win, although we will play in the best way possible.

In American Blackjack the percentages are slightly different but in no case exceed 1%, as long as you apply a basic strategy adapted to these rules, remember that each mode is different and needs a different basic strategy.

Basic Strategy Analysis

If the optimal way to play only minimizes losses, is there a real way to win at blackjack?

To answer this question we must understand what hypotheses have been made to solve this problem.

The basic strategy was developed taking into account that the odds of any card are invariable throughout the game, i.e. the probability that an ace, a number or a figure will appear are always the same. This is not entirely real since since we know that the odds are changing while the cards are being dealt.

But what would happen if I told you that we can have a system to count these cards, and anticipate more winning hands?

6.Counting Cards (HI-LO system)

This counting system is known as HI-Lo and was first written in 1962 by a former IBM employee mathematician in the book “Beat the dealer

The idea is to control the high cards in the deck, which are the only ones that can make up blackjack, so that if we know how many high cards have appeared we know if there are many or few left to appear, and so we can know what the chances are of getting blackjack in real time, with the additional advantage that this entails.

To know that advantage we need to have a control over the cards that are appearing, something that seems to be quite complicated if for this we need to memorize all the cards that are appearing. Fortunately, mathematics offers us a better solution.

The Hi-Lo system associates the cards to three different values -1, 0 and 1.

1 negative to high cards, 1 positive to low cards and the remaining cards acquire a zero value or 0.

Our task is then to keep track of all the cards that have been dealt including the dealer’s.

Since in this system there is the same proportion of high and low cards, a positive or negative count tells us directly when there are no more high cards left in the deck.

So if our count is negative it is because we will have counted more high cards, and there will be fewer high cards left to appear, something that does not interest us.

On the other hand, if our count is positive, it is because we will have counted more low cards, and we will know for sure that there are more high cards to appear. It is here where we can take advantage.

Our objective with this system is to accumulate in that account a positive number as big as possible that offers us the biggest probabilities of obtaining blackjack. If we achieve this we can say that the table is hot and we can modify the basic strategy to our interest for example to double the bet or to bet for sure. As blackjack pays out 3 to 2 and cases of ties are unlikely we have for the first time a game system with an expected profit higher than the bank’s. And all thanks to mathematics.

Notice that the low cards balance out the high ones, which means that the total count once all the cards have been dealt has to be 0 obligatorily. Besides we also see that there are 3 cards that are not considered neither high nor low, this is because the system has to balance 5 high with 5 low, but in the deck there are more numbers than aces and tens so there are 3 leftover numbers that are grouped in a neutral value that does not interfere on the sum.

In the case of playing with several decks you have to take into account that it is not the same a sum with 4 pending decks than the same sum with 1. That’s why you have to go divide the current sum by the number of decks that we think are left to go out, and this will be the real account.

There are other counting methods a little more efficient but they assign more values and are a little more complicated to execute, but if you understand the HI-LO you will understand any other.

Although we can have an advantage with this system all this happens after thousands and thousands of hands and it gives us an advantage of tenths of percentage, so you are going to need a very big wallet and a lot of time.

Current measures against Card Counting

Unfortunately, casinos have introduced measures to counteract card counters.

-The first one is to increase the number of decks, and that is that the more decks you use the more complicated game you will have to win by counting. Think that the fact that there are more decks pending makes it more difficult to accumulate only the best cards at the end than with a single deck, that makes the variance of the count you are carrying is smaller and consequently you have less chances.

One: 0,17%

Two: 0.46%

Four: 0.60%

Six: 0.64%

Eight: 0.66%

-The second measure that is currently applied are the mixers and automatic elements to shuffle the cards before the end of the game, which force the counter to restart the account that had been accumulated and therefore lose all the advantage.

-In addition some casinos like in Las Vegas pay 6 to 5 for blackjack which triples the house advantage over the player and even in some if they suspect that a player is a counter they can afford to modify the house bet.

You have to know that the counting is legal but if you are caught you will be expelled from the casino. The casinos know the profile of an accountant so it won’t be too difficult for them to discover you if you start to win money.

7.Final Conclusions

From the point of view of numbers if there is a mathematical chance of winning at blackjack that’s why many people have won money, but it’s not easy to execute, not fast, not even cheap so it’s probably not within your reach.

In any case if you are going to play:

• I recommend you to learn and adapt first the basic strategy to improve your chances.
• Do not bet on tables with payouts lower than 3 to 2.
• Play at tables with the smallest possible number of decks and check the table rules very well.
• And if you are going to count cards, study how they are shuffled and test your strategy first before investing a large amount.

Remember that:

• The more decks, the more the house wins.
• The worse the rules, the more the house wins.
• And the less strategy or knowledge you have, the faster and safer the house wins.

So the house always wins?

It does not always win, but it is clear that if it does not, it will change whatever is necessary to do so. Remember that this is a business.