The Monty Hall Problem
NOTICE: This article does not intend to promote gambling or ludopathy. It is an analysis focused on the mathematics of gambling, where it is explained whether gambling can be profitable or not and how to analyze it.
Welcome to one of the most curious problems in mathematics, the Monty Hall problem.
1.Description of the problem
2.Intuitive analysis
3.Monty Hall Simulator
4.Mathematical Analysis
4.1.Mathematical Analysis with Conditional Probability
5.Intuitive solution
6.Explanation
7.Conclusions
1.Description of the problem
Imagine you are in a contest and I am the presenter
Behind one of these 3 doors is a new car. And behind the other two there are goats (yes goats!!).
You have to choose a door and we will assume that for example you choose the door 1 (remember that you have to win the new car and not a goat …)
I who can see what is behind each door discard one of the doors that has a goat, opening the number 3 in this case, and now I ask you the following question, do you want to change the door 1 by 2?, or more importantly for the purpose of this video, do you think that matters?
The Monty Hall problem is one of the most famous problems of probability and comes from the television contest of the 70’s Let’s Make a Deal. The name refers to its famous presenter, and his well-known 3-door game. Where a car was hidden between one of them, and the contestant had to choose a door. After discarding another of the doors, Monty Hall asked the contestant if he wanted to change the door or keep the one he had chosen. And this is where the real game begins.
2.Intuitive analysis
I’m sure many of you think there’s no difference between keeping the door or changing it. If there are two doors and a car left, either option is the same as if you change the door you can win or lose the car and if you don’t change it you can also win or lose, which leaves each door with a 50% chance. But, is that true?
Your intuition may tell you that it is, but do you think your intuition has analyzed the problem correctly, do you think you can trust your instinct?
3.Monty Hall Simulator
To get out of doubts I have created a simulator that recreates the rules of this game and we will see what results it offers us for both elections, so, don’t miss it:
It does exactly what we have described, so we start playing and ask us to choose a door, we choose it and the presenter opens another door where the car is not. Then he makes us choose between changing the door or keeping it.
Always keeping the door:
Let’s try first to stay the door we have chosen, so we play many games to the simulator, and we conclude that we win the car about 30% of the times we have played (which shows us the success rate).
Always changing the door:
If instead we choose to change our door for the other one, and we repeat this many times in the simulator, we come to the conclusion that this time we win the car about 60% of the times. Which makes both results very different.
Don’t you believe it? Try it yourself
We thought it wouldn’t matter, but we have seen that changing doors makes us winners in a higher percentage than keeping the door we had, and it seems to be quite superior. So what’s going on?
4.Mathematical Analysis
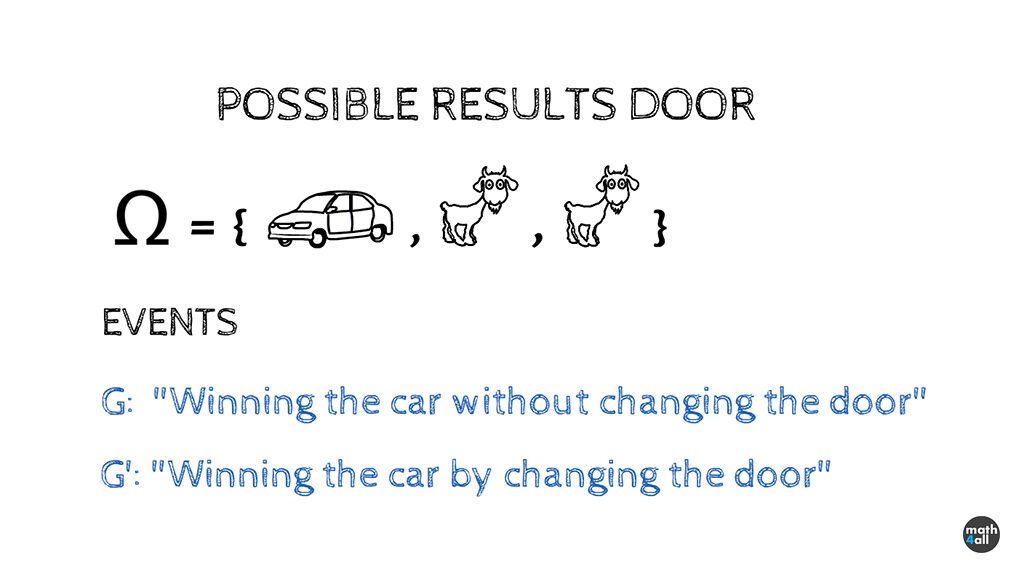
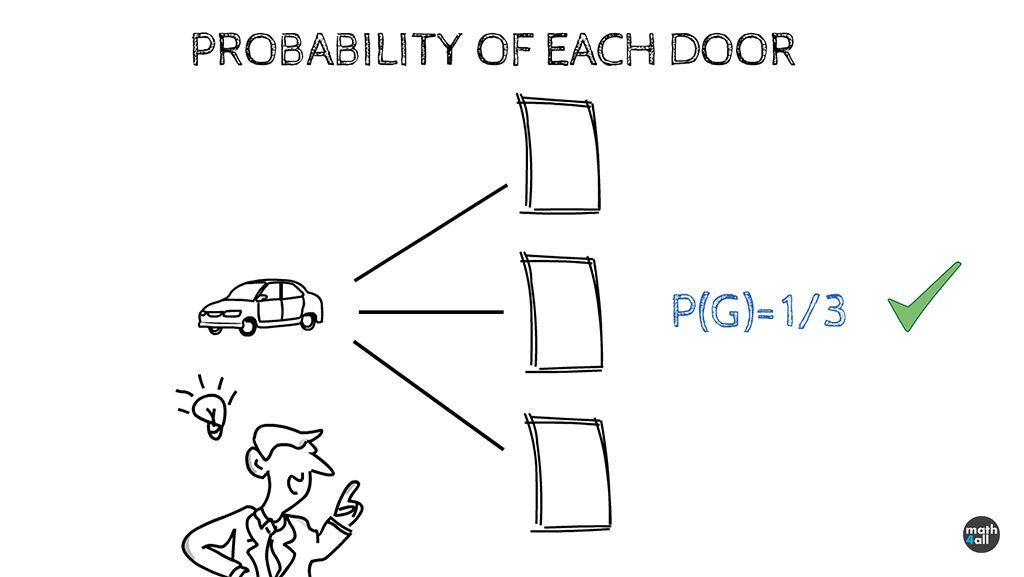
If we analyze the problem at a mathematical level we will realize that this is a simple probability problem, where all the possible results of the experiment of choosing a door are 3:
choose car, choose a goat, or choose the other goat.
The events we need to solve the problem are:
G: “Win the car without changing the door”
G’: “Win the car by changing the door”
We will study the probability of each event separately:
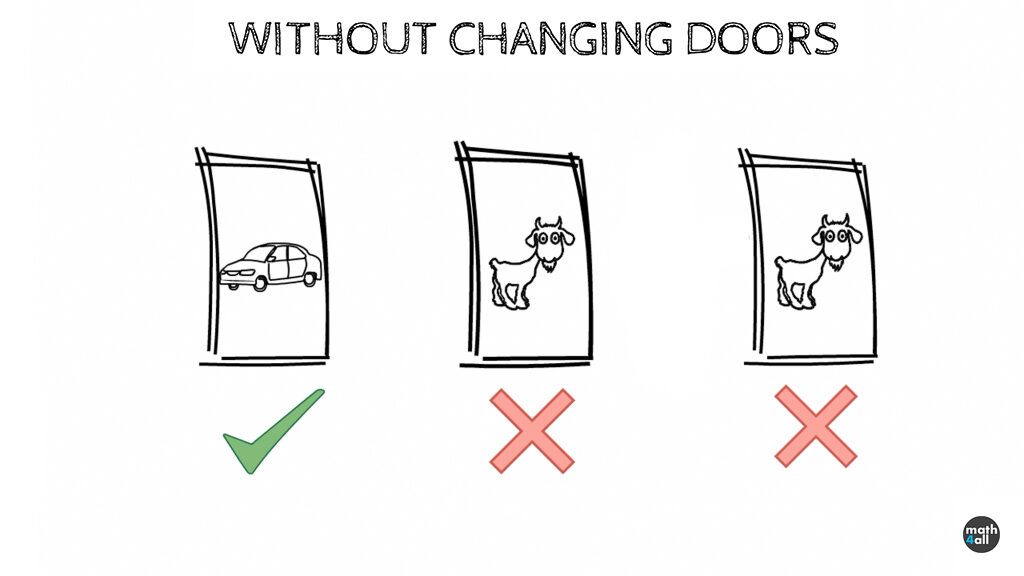
Without changing the door
So let’s start by not changing the doors.
If the contestant chooses the car, and doesn’t change the door, the car will win for sure, because it will hold its door until the end.
In the same way if the contestant chooses a goat, and doesn’t change the door, he will never be able to win the car.
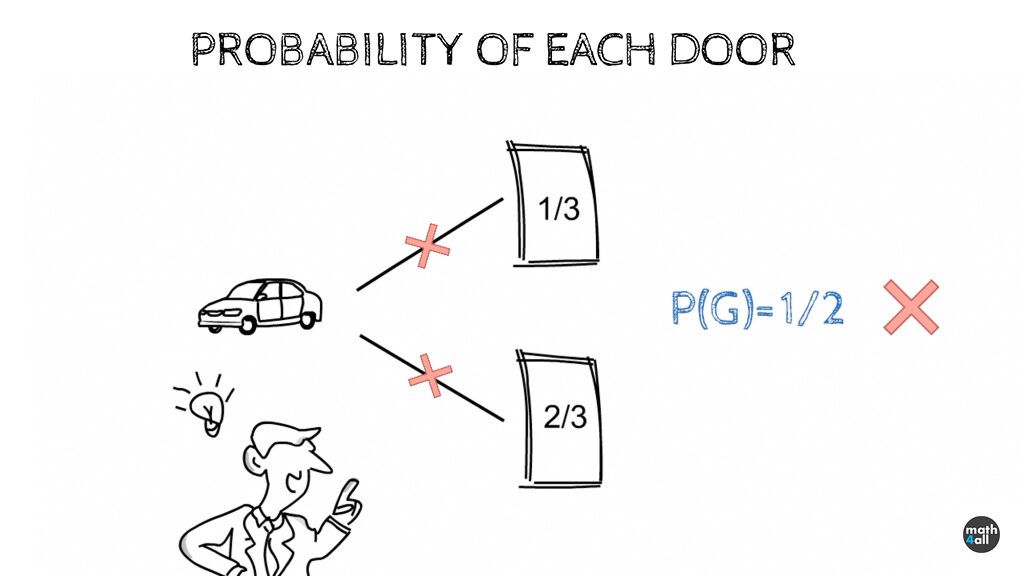
As there is only 1 case where he wins out of 3 possible choices, the probability of winning the car if he doesn’t change the door is 1/3. This is approximately a 33.33% chance of winning. That’s 1 in 3 times, which leaves you at a disadvantage to win the car.
Let’s see now what the probability is if you decide to change doors:
Changing Door
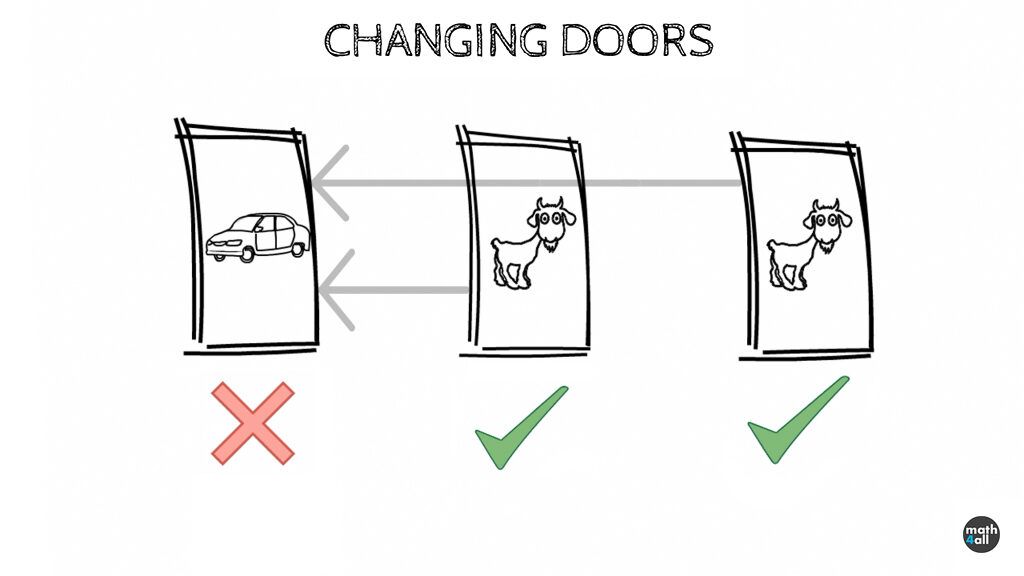
If the contestant chooses the car, and changes the door, he will never be able to win it since he will always change it for a goat. It doesn’t seem like a good start.
Instead, notice that if he chooses a goat, the host always shows him the other goat. This automatically discards one of the goats, which means that the contestant will have to change the goat he has obligatorily for the car. As there are 2 goats as possible choices we will win the car 2 out of 3 times so the probability of winning the car by changing doors 2/3. This doubles the probabilities from 33.33 to 66.66%. This gives us a greater advantage to win the car.
4.1.Mathematical Analysis with Conditional Probability
The events we need to solve the problem are:
A: The contestant chooses the door where the car is”
B: “The contestant chooses the door where there is a goat”
And finally the event we are looking for that is:
G: “The contestant win the car”
The probability of choosing the door with the car as you see is 1 in 3, and that of choosing the door with a goat is 2/3 , but what is the probability of winning?
P(A)=1/3
P(B)=2/3
P(G)=?
To win we can do it either way. Choose the car and win or choose a goat and win, therefore
P(G)= P((A and G) or (B and G))
What translated into mathematical language is:
P(G)=P((A∩G) ∪ (B∩G)) (You simply have to change the symbols of and for intersection and the or for union)
Well, the probability of a union is the sum of probabilities so we can separate the probability into 2 simpler ones
P(G)=P(A∩G) + P(B∩G)
If we use the conditional probability formula and clear the intersection we have left:
P(G)=P(G|A)·P(A) + P(G|B)·P(B)
Now we only have to calculate the probability of winning for each strategy:
Probability without changing Door
If we have decided to keep the door we had:
In the case of having a car, we will have won for sure, since we are not going to change it, so the conditional probability of that event A, will be 100% or 1
P(G|A)=1
But this will only happen when we have a car and we have 1/3 chance of choosing it, so the probability of choosing the car and winning is 1·1/3 which is 1/3
P(A)=1/3
P(A∩G)=P(G|A)·P(A)=1·1/3=1/3
In the case of having a goat, if we keep the door we will never win so the conditional probability of the event will be 0, and when we multiply it by the probabilities of having a goat it’s still 0, which is logical if we already see that it is impossible to choose the goat and win the car from the beginning.
P(G|B)=0
P(B)=2/3
P(B∩G)=P(G|B)·P(B)=0·2/3=0
If we add both amounts we have a 1/3 chance of winning if we keep the door.
P(G)=P(A∩G) + P(B∩G)=1/3 + 0=1/3
This can be summarized as (Car,Goat,Goat)
Probability of Changing Door
Let’s now choose to change the door always:
In the case of having a car, we lose the car for sure, since we are going to change it for a goat, so the probability conditioned to that event A, will be 0
P(G|A)=0
And the probability of taking the car and winning will be 0.
P(A)=1/3
P(A∩G)=P(G|A)·P(A)=0·1/3=0
If instead we choose a goat, notice that the presenter always eliminates the other goat, so there will only be the car when we change the door, so we will always win the car.
P(G|B)=1
This will only happen when we have a goat, but we have to consider that the probability of choosing a goat is 2/3, so the probability of having a goat and winning is 1·2/3 which is 2/3
P(B)=2/3
P(B∩G)=P(G|B)·P(B)=1·2/3=2/3
If we add both amounts we have that the probability of winning if we change doors is 2/3
P(G)=P(A∩G) + P(B∩G)=0 + 2/3=2/3
This can be summarized as (Goat,Car,Car)
5.Intuitive solution
If we don’t change the door we see clearly that as there are two goats and a car we have a 1/3 chance of winning the car.
If we change the door:
- and we choose the car we always lose.
- and we choose a goat we always win.
But as there is 1 car and 2 goats, we will win twice out of 3 times, because 2 out of 3 times we will choose a goat.
6.Explanation
For this we are going to imagine again all the possible cases that can occur for the 3 doors. (Note that we don’t differentiate the order of the goats, since that doubles the number of cases, but doesn’t change the probabilities)
When we choose our door, we have a 1/3 chance of having the car. Even if the presenter opens a door, it is conditioned by the one we have chosen, since he can only open a door that is not ours. That implies that he always removes a goat from the other two doors, but never from ours.
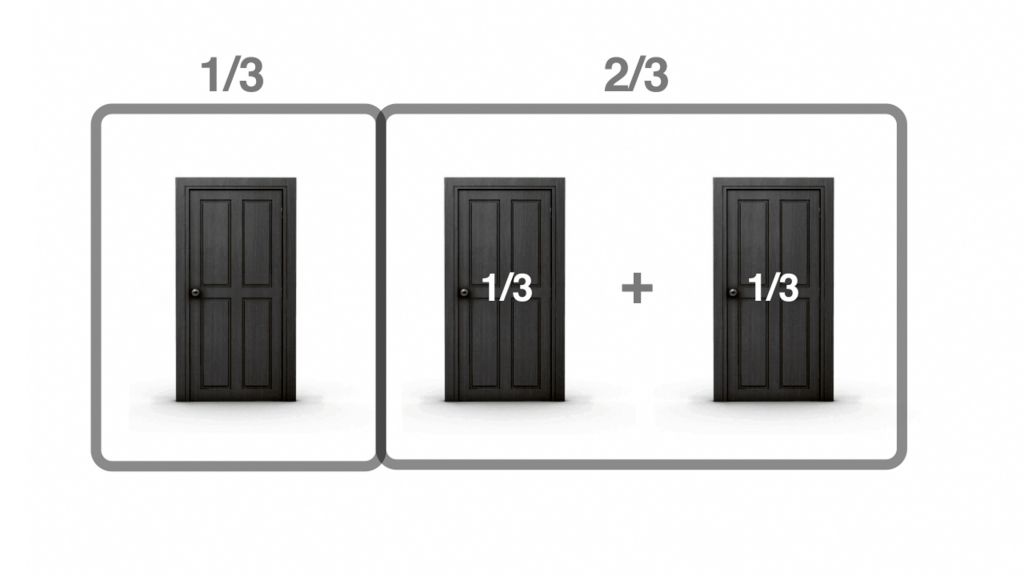
Notice also that in those 2 doors there is always a goat to be eliminated, so the presenter only discards a goat that was safe and shows us where it is, but that does not increase the probabilities of our door, since we can still have the other goat the same times. This implies that the door we chose at the beginning will still have the car 1 out of 3 times and will not increase its probabilities, no matter how much we remove a door.
Surprising, that doesn’t change, but then what about the other door?
If our door has the car 1 out of 3 times, the other 2 times will be in the other two doors, so that group of 2 is logically more likely to have the car than our door. We simply have to add up the probability of each one.
When the presenter opens a door, he knows what’s behind each one, so he always saves the car if he has one. If both doors have the car 2 out of 3 times and always discards a goat, the door that is saved will still have the car 2 out of 3 times, so its probability will be the same as both doors had but spread out in one. So you must change it for this one.
Note also that this door will not always be the same and therefore has more probability.
And that said, are you sure you don’t want to change doors?
Expansion of the idea
Imagine now the same game but with 20 doors instead of 3. We keep choosing 1 door, and the presenter eliminates in the same way the doors that are goat until he gets one.
If we forget our door for a moment, and think only of the 19 that can be eliminated by the presenter. We will see very clearly that 19 doors are much more likely than one, so the car will be most of the time in one of the doors that the presenter has and only one in our door. And if the presenter eliminates all the doors that are goat of that group, the remaining door will have the car most of the time, in the same way.
7.Conclusions
In conclusion, the presenter only eliminates goats from his doors, and that can only give an advantage to some of his doors, but never to ours.
As we saw at the end it wasn’t that complicated either, but why haven’t we been able to see it before?
At first the car can be equally on any of the doors, so we divide 1 prize between 3 doors, and so we calculated the probability for our door. So far so good.
The problem comes when they open a door for us.
When the presenter gives us the option of keeping our door or changing it, we must recalculate the probability of each door to know which one is more convenient for us. To do this, we divide 1 prize between 2 doors in the same way as before, as if the prize could be the same in each one of them, but this is not the case, since the discard that the presenter makes only increases the probability of the door he is going to offer you and not of both equally. This is why the calculation is incorrect. (66%>33%)
Note that the only way to have a 50% chance of winning, is to choose to change doors or not at random, because in this case although one door is more likely, we have the same options to choose it as the other, so the times we change doors, will compensate for the times we do not. In any case, this is still less than always changing the door, although more than always keeping the door. (66%>50%>33%)
Curious, isn’t it?
We now know that Monty Hall was a very clever guy, using psychology and mathematics. If the contestant didn’t change doors, he had the chance to lose, and to gain an advantage he had to “take risks” and accept the change.
The reality is that most contestants lost their car, because very few people dared to change the door. Who would change a door when the question can be a trap? Only a madman, or a mathematician, and that’s what cheating is all about.
Who says math is useless?
If you are interested in the math of the game you can visit my youtube channel math for all on Youtube where I study mathematical games of chance like Poker or Blackjack.
