The Mathematics of Poker – Odds and Outs
Do you think math is important in poker? In this article I will analyze poker on a mathematical level so that you know how to calculate your probabilities, analyze your actions, or how mathematics can make you a better player.
1.Texas Holdem Poker Rules
2.Texas Holdem Poker Hands
3.Texas Holdem Poker Actions
4.Texas Holdem Poker Probabilities
5.Poker as a game of incomplete and imperfect information
6.Odds and Outs
7.Texas Holdem Poker Calculator
1.Texas Holdem Poker Rules
Texas hold’em unlimited poker is a French card game with up to 23 players simultaneously, where the objective is to eliminate all players from the table, to win all their chips, or simply to win as much money as possible in cash mode. For this, 2 non-visible cards are dealt to each player, and they will decide in turns and based on their cards, if they want to bet, check, fold, call or raise.
Once all players have made a decision, the dealer draws 3 visible flop cards, which are used by each player to bind their cards in order to get the best possible hand, and proceeds to a new round of betting.
As the dealer uncovers a new card, the same procedure is repeated until finally 5 cards are uncovered. Finally, the players still at the table show their cards and the winner of the pot is the player with the best hand. The players must use their knowledge and their strategy to make the best decisions that will allow them to win.
2.Texas Holdem Poker Hands
- Pair: First of all, we have the pair, which is the most basic hand in poker formed by 2 cards of different suits that have the same value. If both players have a pair, the one with the highest value wins, and if that value is the same, the player with the highest card wins. The pair is the least valuable hand that can be linked.
- Double Pair: The double pair is composed of 2 different pairs together with any other card. If both players have a double pair, the hand with the highest pair wins, and in case of a tie, the unmatched card with the highest value wins
- Three of a kind: As its name indicates, the trio is 3 cards of different suits with the same value, together with 2 cards of any kind. In case both players have a trio, the one with the highest value wins. Note that in this modality of Poker there cannot be 2 trios of the same value, since there are only 4 possible suits and with one there are already 3.
- Straight: The Straight is made up of 5 consecutive cards of the same suit or different suits, so all the values can be ordered one by one from lower to higher. Depending on the number of cards you start with, you will have a higher or lower straight, so in case of a tie, the one with higher values will always win.
- Flush: There are 5 cards of the same suit regardless of their value. In case of a draw, the flush with the highest card wins.
Full/Full house: Gather 3 cards of the same value and 2 cards of another, or what is the same, a trio and a pair simultaneously. When two players have a full house, the value of the highest trio wins. - Four of kind: It’s composed of a quartet of 4 cards of different suits that have the same value, together with any card. In case of a draw the value of that card decides the winner. Although this is the most popular hand, it is not the most valuable.
- Straight Flush: It’s a straight flush made up of all the lower cards of the same suit, which makes it a rather unlikely move. When two players have a straight flush, the straight with the highest values wins.
- Five of a kind (Royal Flush): This is the best poker move and is composed of all the high cards of the same suit which are 10,J,Q,K and As. In case there are 2 simultaneous hands like this one, none of the players would win, although if you think about it, it is almost impossible to have 2 simultaneous royal flushes.
- All the hands you have seen are ordered by ranking from least to most, so you also know who would win when two different hands meet. In the event that no player manages to form either of these hands, the one with the highest card wins, and in the hypothetical case of having the same, the one with the next highest card wins.
3.Texas Holdem Poker Actions
Now that you’ve seen all the hands and their priority, let’s review what actions you can take within the betting round, so don’t miss out!
- Betting: Bets are placed in turns clockwise, and players who bet later must match the amount (call) bet at least to stay in the hand. But you can also raise if you want to force the other players to stay in the hand, and if you do so they must match the amount again until the raise is matched. (It’s like a tug-of-war).
- All-in betting: When a player bets all his chips in a hand, it is said that he is all-in, and (if another player bets a larger amount), a separate pot is created in which the player is not. If more than one player goes all in in the same hand, different pots will be accumulated. To go all in you need to have a good feeling because you risk losing all your chips.
- Betting Blinds: In the hold’em mode there are two players obliged to bet a minimum amount at the beginning of each round, which are the blinds. These are the blinds. The blinds change players in each hand, with the objective that all have equal losses/the same losses at the end. The Big Blind is equivalent to the minimum bet for that round and the Small Blind is usually half the Big Blind, but this can change. These blinds are posted consecutively to the left of the dealer, first the Small and then the Big, and are intended to force players who want to enter the hand with a minimum amount. In the tournaments the blinds are increased in quantity to accelerate the speed of the games.
- Check: When no player has made any bets in that round or the bet amount has already been matched, you can choose stay or “check” if you consider that it is not necessary to open or raise the bet with your cards. This allows you to remain in the hand, without making any extra bets.
- Checkout: The player always has the option to check out if he feels he has no options in that hand, and will lose his cards and the amount he had bet up to that point, with no possibility of re-entering.
You’ve seen what actions you can take, and what hands there are, but what chances do you think you have of linking any? Do you think it’s easy to get a straight or a poker?
4.Texas Holdem Poker Probabilities
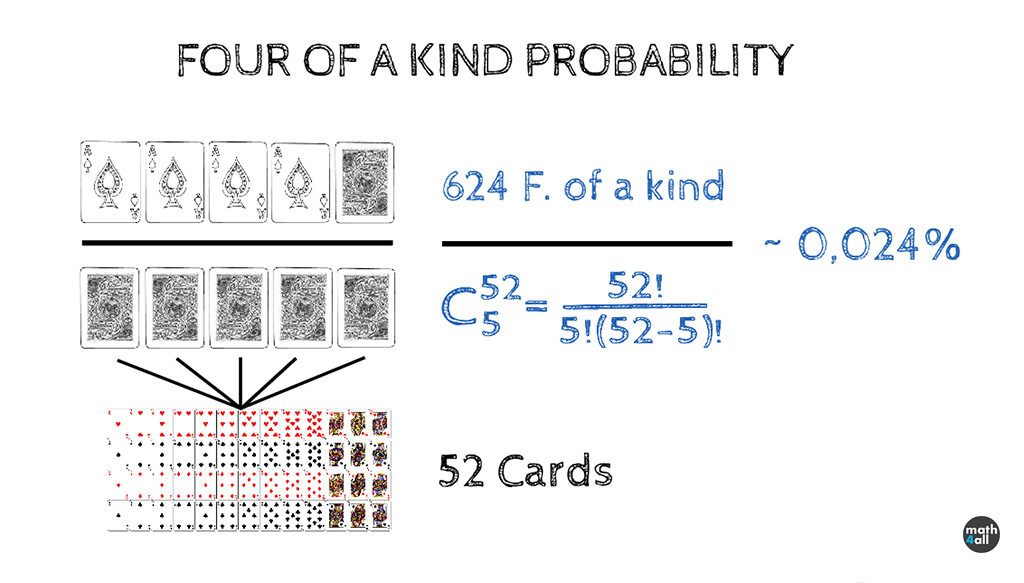
Let’s calculate the probabilities of a Four of a Kind. To tie this hand you need 4 cards of the same value out of 5 cards that are dealt. That is: The ways you have to get 4 equal cards (with 1 possible value of 13 and 4 possible suits of 4) by the ways to get another card that is not of that value, (with 1 possible value of the remaining 12 remaining, and logically 1 suit of 4). What it actually calculates for both, are the ways to select the values by the ways to select the suits.
This gives us exactly 624 total possible ways to make Four of Kind from all the combinations you can make, but how many are there?
If we take into account that a French deck has 52 cards and you must select 5 cards, the total number of possibilities are all the possible combinations of 52 elements taken in 5 since if you think about it carefully (and not like in this video) the order does not matter and they cannot be repeated. (but this is better thought out by you)
This calculation indicates that the probability of linking a Four of a Kind before uncovering any cards is approximately 0.02%, which means that you have very little chance a priori of linking it as it’s a very unlikely hand. But what do you think are the probabilities of the other hands?
As you see the important hands like Four of a Kind or Full House are the most difficult to get, and vice versa, the less important hands are much easier and more likely, which makes sense. Note also that the only hand you can often aspire to is a pair, as hands such as three of a kind, flush or even double pair are quite complicated to achieve.
The most important thing is that none of the hands reaches 50%, and not even the sum of all of them gets 50%, which means that most of the time you are not going to get anything, although this gives you some clues on how to approach the game. Was this what you imagined?
You have already seen that to get a good hand is not easy, then what you will have normally will be cards that can conform a hand with the cards that are left to uncover, or what is the same a hand draw, this will be able to be completed or not with certain probability. But how do you calculate?
5.Poker as a game of incomplete and imperfect information
If you have ever watched a poker tournament on TV, you will surely remember a percentage that is shown next to each player’s cards. This is nothing more than the probability each player has of winning and is based on both his cards and those of the other players, including the community cards. If we think about it, this calculation is only possible because the television knows the cards of each and every one of them, so only we can see what real probabilities they have and who is playing better.
If the players could know the hand of their rivals, they wouldn’t have any difficulty to play as they could calculate these probabilities in an exact way, but unfortunately this is not possible, because we don’t know what cards they have, that’s why poker is considered a game of incomplete and imperfect information. Consequently the players have to try to collect all the possible information, to calculate something that approaches as much as possible to those probabilities.
6.Odds and Outs
For this we must introduce two mathematical concepts that are used in the world of Poker that are the odds and outs, and that serve to calculate the probabilities of completing a draw or draws.
Imagine that you have a flush draw in your turn and you want to calculate the probabilities of being able to complete it in the last betting round.
To complete you draw with the following card you need one that is of the same suit. Since a suit has 13 cards and 4 of them have already come out, there are only 9 cards left in the deck that would serve to complete your flush, and this gives a total of 9 outs.
If we want to calculate the probabilities for those 9 outs, what we will do is calculate the odds, which is the probability used in poker and unlike the usual one, where favorable cases are calculated among the possible ones, here the unfavorable ones are calculated among the favorable ones. And why like that? Because normally we have more probabilities of not linking our draw than of linking it, but this you will see later.
The favorable cases are precisely the outs and the unfavorable are all possible cases except the favorable (ie all except the outs). Finally, the possible cases are the amount of cards that remain to be shown, which we calculate by subtracting from the 52 total cards of the deck, those that have already been uncovered including also those of the rivals. If you do the calculation for your 9 outs, you will get an odds of 4.11, or in other words, for every time you win you will lose 4.11 times, which is equivalent to a 19.57% probability of linking the flush with the last card to be drawn. What do you think?
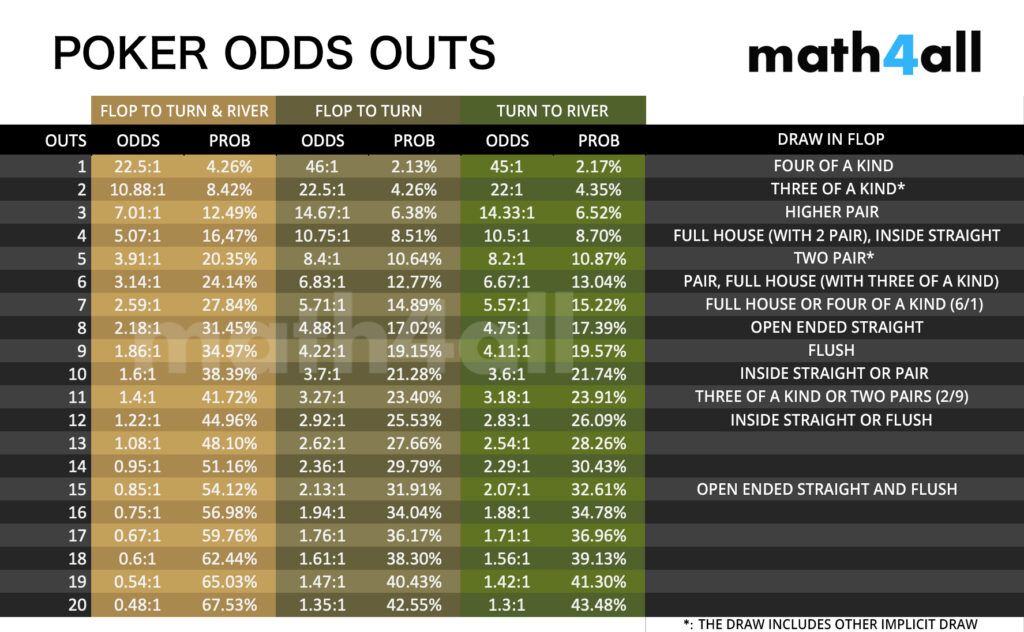
Calculating all this is not very practical, so I have created a chart, where you can check what odds you have with the outs of your draw or draws.
If you take a look you can see the table is basically composed of 3 columns, which are the probabilities that can be calculated in the stages of flop and turn ordered from left to right, where we are mainly interested in the first and last.
If we want to consult our flush draw with 9 outs in the turn we see the same 4.11 that we had calculated on our own.
With these tables you can see interesting things, like that a flush draw has more probabilities than any straight draw, or that a straight draw has more probabilities if it can be completed by two points instead of one.
Notice also that any draw that includes 2 simultaneous hands (like a straight and flush draw at the same time) is always going to be more likely than either of those two separate draws. Since it can be completed in either way, it accepts a greater number of outs. Curious, isn’t it?
Another important detail is that you will almost never have more than a 50% chance, which indicates as I said before that most of the time you will not link your draw. (Even if you don’t throw in the towel yet)
On a practical level, you can calculate all this, without the need for tables, with the rule of 4 and the rule of 2 (multiplying by 4 in the flop a turn and river and by 2 in the turn). These rules provide a fairly close value and can be useful when we do not have anything at hand. If you use them for your draw, your 9 outs in the turn are (9 x 2 = 18%) which is very close to the 19.57% shown in the table. This can be enough for many players, although there are other similar rules to approximate these values. There are also different odds variants if you are interested in the subject.
After seeing all this you could ask yourself the following questions:
- If we normally have a small chance, what’s the point of betting, shouldn’t we do it only when we have a majority of possibilities?
- Even if we are calculating the odds for our draw, can’t the rival beat us with a higher draw? Or in other words, how much difference is there between calculating our odds and the real odds?
7.Texas Holdem Poker Calculator
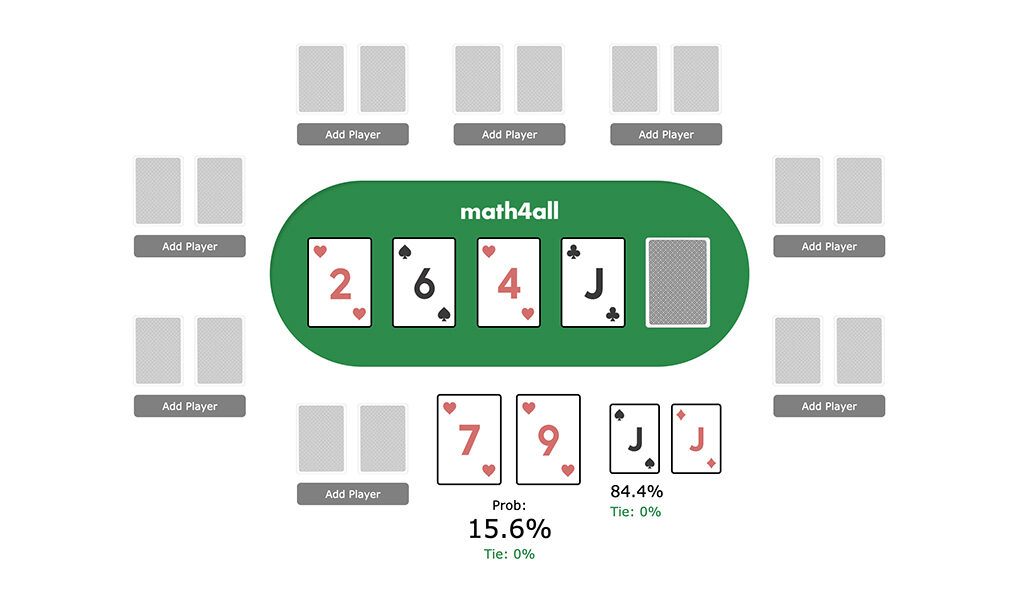
To solve your doubts I have created a Poker Calculator where we are going to experiment a little bit with all these concepts.
With it you can see that a simple pair of 77’s has more probabilities in front of an ace, k, or that a straight and flush draw has more probabilities than a brand new pair of kings on the flop.
You can also see that a pair with low values like 66 is not as good a hand either, as it can be easily outdone by any higher pair. You can consult any hand you need.
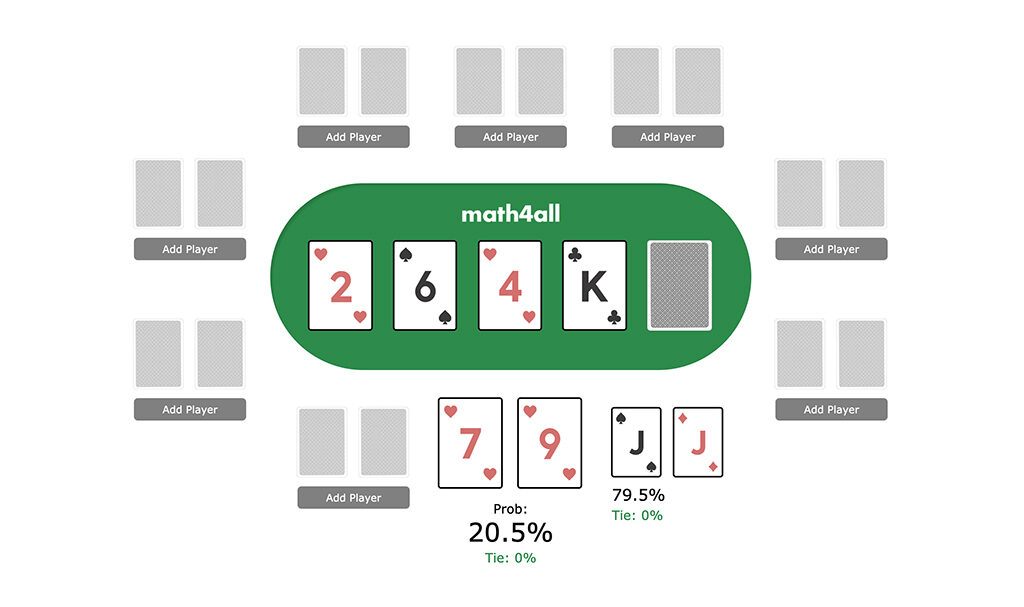
Now let’s create with our Poker Calculator your flush draw. And let’s suppose that your opponent aspires to an inferior draw with a pair of J’s. We press the button to calculate the result and we see that your chances of winning against their cards are 20% which is quite similar to what we had calculated.
It may seem that the odds are enough to know for sure our probabilities. But imagine that the cards would allow your opponent to have a superior draw like Poker or Full House. If we recalculate your probabilities for this possible situation, we see that the calculation no longer fits the odds. This happens because before, your probability of winning depended only on whether or not you picked up your draw, but now you also depend on whether or not your opponent gets a higher draw, which decreases your options as you can be beaten with a better hand than the flush.
Things are getting interesting…
Note that the most important detail is that although the calculation is different, it’s not too big a difference, because it is still more difficult to link a Full or Four of a kind than a flush. This indicates that the stronger your hand draw is, the more reliable your odds will be on average, since it will be more difficult for another draw to modify them. Depending more on ourselves gives us more complete information, and we must take advantage of it.
But in practice it is easy that your opponents can have better cards than you, especially when there are many players at the table or big bets are made, that’s why you should also always have in mind the possible draws or hands that your opponents can have with the community cards, especially when a big amount of money is bet.
When your tied hand is superior to all those possible ones, your victory will be assured, but when you have only one draw and there can’t be higher hands with the cards that are left to reveal, your real probabilities will be at least your odds (calculated probability).