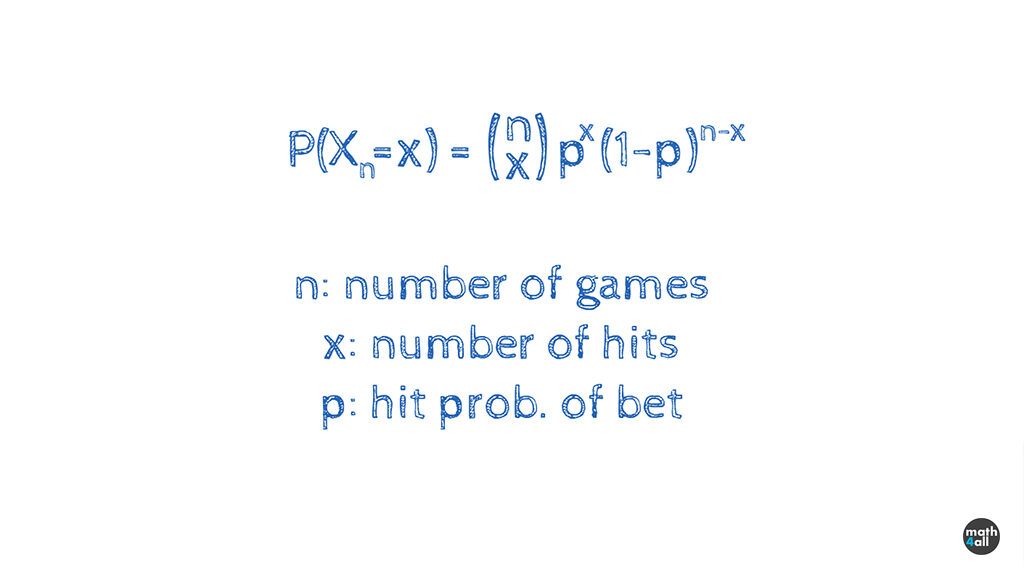The Mathematics of Roulette

Do you think you can win in Roulette? In this article I will analyze the game of roulette on a mathematical level so that you know whether or not it is possible to win in the long run. Are you ready?

1.Roulette Rules
 1.1.Roulette Bets
2.Mathematical Study of the Roulette
 2.1.Expectation of Straight Up
 2.2.Profit Expectation of Straight Up
 2.3.Profit Expectation of All Bets
 2.4.Simulation with real Money
3.Frequently Asked Questions
4.Conclusions

1.Roulette Rules

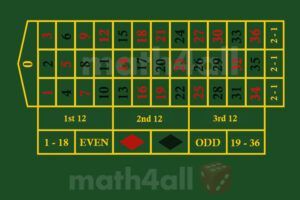
-The European Roulette is made up of 37 spinning numbers and a ball is thrown which falls into one of them.

-Bets can be made on based on a number, or a group of numbers, and are rewarded differently.

–18 of the numbers are red and the other 18 are black which added to 0 gives us 37.

-Half of these numbers are even and the other odd, except 0 or 00 which is considered neither even nor odd in this game.

-In American Roulette you have one more number which is double zero but in this video we will focus on European Roulette with one zero.

-The bets can be made with the roulette stopped or in movement since the croupier or the machine indicates “place your bets” and until indicates “no more bets“.

-Once the ball has landed on the number, those who have hit it are rewarded and the dealer keeps the remaining chips from the players who have lost their bets.

Roulette Bets

Let’s see now all the bets or plays of the European roulette to which you can bet and what are their probability (not the odds as some pages show, odds and probability are related but are not the same):

Simple Bets

• Red-Black: 1 to 1 (probability 18/37 =~ 48.6%) (47.4% American Roulette)

• Even-Odd: 1 to 1 (probability 18/37 =~ 48.6%) (47.4% American Roulette)

• Low-High (1-18/19-36):  1 to 1 (probability 18/37 =~ 48.6%) (47.4% American Roulette)

Multiple Bets

• Double Dozen: 1/2  to 1 (probability 24/37 =~ 64.8%) (63,1% American Roulette)

• Double Column: 1/2 to 1 (probability 24/37 =~ 64.8%) (63,1% American Roulette)

• Dozen: 2 to 1 (probability 12/37=~  32.4%) (31.6% American Roulette)

• Column: 2 to 1 (probability 12/37 =~ 32.4%) (31.6% American Roulette)

• Line/6 number: 5 to 1 (probability 6/37 =~ 16.2%) (15.8% American Roulette)

• Corner: 8 to 1 (probability 4/37 =~ 10.8%) (10.5% American Roulette)

• Street: 11 to 1 (probability 6/37 =~ 8.1%) (7.9% American Roulette)

• Split: 17 to 1 (probability 2/37 =~ 5.4%) (5.3% American Roulette)

• Straight Up: 35 to 1 (probability 1/37 =~ 2.7%) (2.60% American Roulette)

As we have seen, both Simple and Multiple bets son realmente are the same at a mathematical level. We have also seen that if a bet is more difficult to hit it is rewarded better.

which raises a number of questions:

-The first one is: is the payout profitable?

-If some bets are easier to hit, but the others have better payout ¿which one is best for us?

2.Mathematical Study of Roulette

If we study Roulette from the mathematical point of view we will realize that any bet is an experiment with 2 possible results success or failure, where the probability of hitting each number is the same regardless of the numbers we take, due to all the numbers have the same probability of appear.

Besides, each game does not depend on the previous one and it doesn’t matter the number that came out before.

In this ideal scenario, the number of hits for a game series, follow a Binomial n,p distribution where n is the game numbers and p the probability of win the bet.

The probability of hitting x times in n games is n combined with x, by p to the x, by (1-p) to the n-x, where p is the probability of winning and (1-p) the probability of loosing.

With this we can calculate the probability of hitting 0,1,2 times or more…

But to know if a bet is profitable we have to know what is the average profit we expect from that bet, so we need to define first the concept of mathematical Expectation.

The expectation for a binomial variable is the number of average hits for n experiments and is calculated as p∙n, in our case it will be the average number of bets won by playing n times.

Expectation of Straight Up

Then the expectation to hit 1 number playing 1 time/game is 1∙(1/37) which is approximately 0.027, that is to say that playing once we are expecting to hit 2.7% on average.

For 2 games will be the same but by 2, which is the 5.4% of hitting.

For 3 games, for 3 games it is the same but by 3,… and thus we can calculate the Expectation for the games that we want.

Notice now that for 37 games the expectation is 1, that is means that playing a Straight 37 times we expect to win once on average, which some of you may have sensed.

Profit Expectation of Straight Up

Now that we know how to calculate the average number of hits for each bet, and the payout, calculating the expected profit for a bet is simple, as it is easy to calculate the average profit and loss.

Expected profit = Expected benefit  – Expected loss

where:

Expected benefit = Expectation(of the bet) · payout · bet

Expected loss = Loss Expectation(of the bet) · payout · bet

So the expected profit for a Straight in 1 game:

is equal to the expectation for a 1 game · payout · bet less the loss expectation for a 1 game · bet:

This is 1/37 · 35 (the payout) · bet – 36/37 · bet, which is about –0.027, In other words, playing once you expect to lose on average the 2.7% of your bet.

and logically the expected margin of the casino or house benefit will be 2.7% of your bet, every time you play.

If you calculate it for 2 games the expected profit is double negative so the casino margin is up to 5.4%.

Then what if we play 37 times?, As we have seen we hope to win once but… what’s the benefit?

In 37 games the winning expectation is 1 and the hope of losing is logically 36, so if you do the calculations you’ll see that the profit is -1 · bet. This means that in 37 games the casino expects to win on average the value of your bet.

This means that if you play a Straight 37 times betting, for example, 1 dollar each time you expect to lose an average of 1 dollar.

Profit Expectation for All Bets

As you’ve seen, playing a Straight doesn’t seem like a very profitable bet, as you lose money in the short and long term. The more money you play, the more money you lose, and you need an average of 37 games to hit only once, but when you do, they pay you with 35 chips which is less money than you spend. Then it doesn’t seem to make much sense to play a single number.

Como vemos, jugar a pleno, además de ser difícil de acertar nos genera pérdidas a corto y a largo plazo. a más jugamos más dinero perdemos y necesitamos jugar en promedio 37 veces para acertar, pero cuando lo hacemos nos pagan 35 que es menos de lo que hemos perdido. Por lo que no parece una buena estrategia jugar a un solo número todo el rato.

The question is, is there a better bet than the Straight?

For this, you need to know what is the profit margin for all the bets, then I’m going to show you some results that I have calculated on my own, so let’s go with them!

Simple Bets

• Red-Black = (18/37∙1)Ap-(18/37∙1)Ap-(1/37∙1/2)Ap = 18/37Ap-19/37Ap = -1/74Ap =~  –1.35% of bet

• Even-Odd = (18/37∙1)Ap-(18/37∙1)Ap-(1/37∙1/2)Ap = 18/37Ap-19/37Ap = -1/74Ap =~  –1.35% of bet

• Low-High = (18/37∙1)Ap-(18/37∙1)Ap-(1/37∙1/2)Ap = 18/37Ap-19/37Ap = -1/74Ap =~  –1.35% of bet

Multiple Bets

• Double Column = (24/37∙0.5)Ap-(13/37∙1)Ap = 12/37Ap-13/37Ap = -1/37Ap  =~  –2.70% of bet

• Double Dozen = (24/37∙0.5)Ap-(13/37∙1)Ap = 12/37Ap-13/37Ap = -1/37Ap  =~ –2.70% of bet

• Column = (12/37∙2)Ap-(25/37∙1)Ap = 24/37A-25/37Ap = -1/37Ap    =~  –2.70% of bet

• Dozen = (12/37∙2)Ap-(25/37∙1)Ap = 24/37A-25/37Ap = -1/37Ap    =~ –2.70% of bet

• Line/6 number = (6/37∙5)Ap-(31/37∙1)Ap = 30/37Ap-31/37Ap = -1/37Ap  =~ –2.70% of bet

• Corner = (4/37∙8)Ap-(33/37∙1)Ap   = 32/37Ap-33/37Ap = -1/37Ap  =~ –2.70% of bet

• Street = (2/37∙17)Ap-(35/37∙1)Ap = 34/37Ap-35/37Ap = -1/37Ap  =~ –2.70% of bet

• Split = (3/37∙11)Ap-(34/37∙1)Ap = 33/37Ap-34/37Ap = -1/37Ap  =~ –2.70% of bet

• Straight Up = (1/37∙35)Ap-(36/37∙1)Ap = 35/37Ap-36/37Ap = -1/37Ap  =~ –2.70% of bet

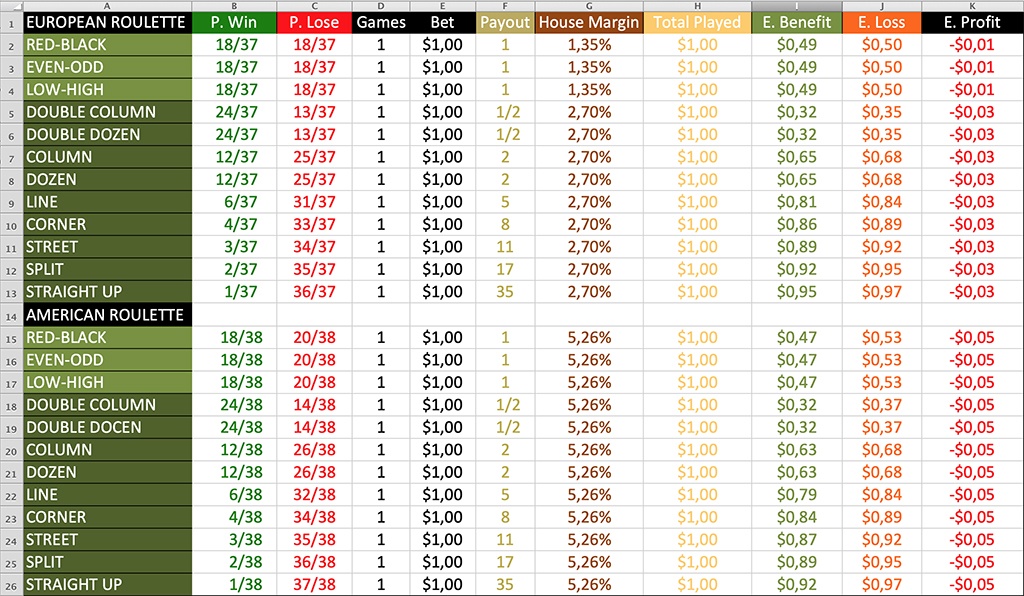
To know what is the casino margin for all bets I have built a spreadsheet and applied the formula you’ve seen for all of them, taking the probability and the payout of each one, to see what is the profit playing once or more times. The most important result obtained is that any simple or multiple bet has the same expected profit in the European Roulette, and the same profit always in the American Roulette. This is because in the European Roulette in the simple bets, if it comes out 0 we lose only the half of the bet and that makes the winnings better. In this way, I have been able to calculate some results. I have caught my attention and that you are going to see next.

 

DOWNLOAD SPREADSHEET

-We see that simple bets are better for us than a Straight or any multiple bet.

-We see that within the single or multiple ones it doesn’t matter the bet you take, if you take two dozens, you will win more times but when you lose you will also lose more, and if you bet a Straight, the payout is bigger, but it will cost you more money to bet it than the payout you will get, that’s why the house margin is the same for all the bets.

Simulation with real Money

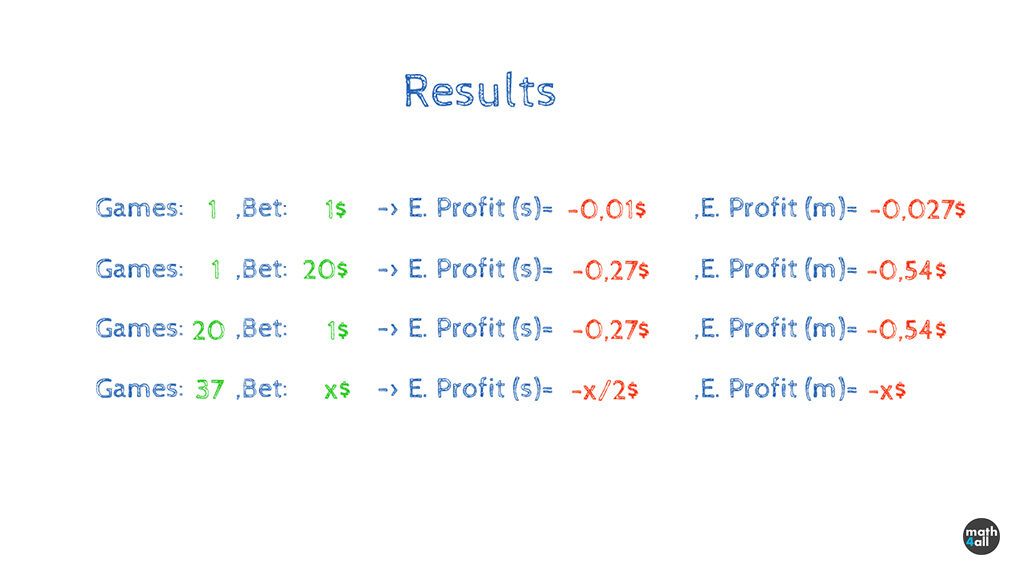
Here’s a simple simulation what would happen with real money:

• 1 game betting 1 dollar/euro: you will lose on average 1 cent in the simple ones and almost 3 cents in the multiple ones (this is because in the simple bets if the 0 comes out, you lose only half of the bet and you have to contemplate that possibility)

• 1 game betting 20 dollars/euros: you will lose 27 cents in the simple ones and 54 cents in the multiple ones, which means that the more money you bet, the more money you lose.

• 20 games betting 1 dollar/euro per game: you lose again 27 and 54 cents. (since it is the same to play 1 time betting 20 dollas that to play 20 times betting 1 dollar), although you have to keep in mind that playing 20 times, your real average will be more similar to those amounts than playing once which means the more times you play the more sure you’ll lose.

• 37 games with any amount: you will lose on average that total amount in any of the multiple ones and half that amount in the simple ones. That is to say, that if you substitute the x by any number you will know how much you are going to lose in average, whatever the bet is.

Keep in mind that these results are for the European Roulette but the American Roulette is even worse because the bets are rewarded the same but you are less likely to get it right because there is one more number. And if you get 0 or 00, you’ll lose everything in this case.

3.Frequently Asked Questions

I have gathered the most interesting questions for a casino player, and thus solved some of your doubts:

QUESTION: If there have been many reds in a row, is it more likely that a black will come out on the next roll?

ANSWER: NO, in fact it is a very common mistake of the players. You have to take into account that roulette is a physical mechanism, which does not remember the results that happend before. That’s why each game is independent from the previous one, and what has to come out will come out, but not the opposite of what has come out before just because we are waiting for it. This is why it is said that roulette has no memory. It is important that you learn to calculate the probabilities correctly. Before playing, many reds or many blacks in a row has a small probability, but once that has happened, what comes next has no more probability or less because it is the opposite, in fact still has the same probability.

QUESTION: What happens if I play several bets at once, such as several numbers at the same time?

ANSWER: Combining bets means that you make several bets at the same time, but it doesn’t mean that they are related, in fact each bet is paid separately. So if you play several bets, the house always pays each bet separately. At a mathematical level if you cover more numbers your probability can increase, but not your profitability. Being independent bets you are making many bets that are not profitable at the same time, and in the end that is even less profitable. Remember that if you want to take a group, a single play also groups numbers and has less margin.

QUESTION: What if I play to double my bet every time I lose?

ANSWER: Doubling the red or black when lost (or any other bet) is known as “martingale”, and has also been studied mathematically. The first thing you should take into account is how many chips you have, and how many times you can afford to double your bet. Keep in mind that doubling implies betting twice as much as you previously lost each time. If you lose a chip, you have to bet 2, then 4, then 8, 16, 32…. and this is an exponential loss growth, which can make you lose all your chips in a relatively short streak of bad luck. The more you maximize the number of times you can double the more you can hold out for the next double, but this can only be done in two ways: either by having a lot of money, or by betting very low value chips. In either case you could win most of the times you visit a casino, but just because you win most of the times doesn’t mean that your balance will be positive in time. Remember that as long as you win you will keep playing. The problem is that mathematically there is a combination of reds or blacks… in a row that exceeds the limit of times you can double with the capital you have (because nobody has infinite money). Surely you think it’s almost impossible to get 10 or 15 reds in a row, and you’re right, it’s quite difficult, but not impossible. The problem is that by playing longer you are increasing the chances of that combination manifesting itself. The more you play, the more likely it is that this will happen, and if it does, you will need to double with money that is no longer of benefit so you can lose all the benefit you had accumulated from playing this and much more. Keep in mind that before playing it is very difficult to get 10 reds in a row, but once you get 9 reds, getting another one is quite simple, because roulette has no memory. Believe me, from experience I know that it is not so complicated to get those strips of red and black in a row, so be very careful with the martingale.

QUESTION: You said earlier that the margin is the same for all multiple plays, but is there a difference?

ANSWER: Actually yes, if you choose a bet difficult to hit like a Straight, you will lose more often and you will need to keep playing to reach the payout or to recover the money you have lost, with which you will play more times on average, and the more you play the more you lose.

QUESTION: And what if I have few chips to bet, what bet would you recommend?

ANSWER: If you have few chips, never take the Straight or any low probability bet, because you won’t have enough chips to cover the average number of shots until you hit. Remember that for a full house you need 37 shots to get an average hit, if you don’t have enough chips most of the time you will leave before hitting one. If you have few chips, make single or probable bets.

QUESTION: Something that has surprised me is that playing a game with 20 dollars is the same as 20 games with 1 dollar, because I like to play, and I don’t understand why I was going to play only 1 game of 20 dollars being able to play 20 and spend more time playing with the same money?

ANSWER: According to this formula, yes, you will earn the same on average, but there is one thing you have overlooked and that is that the average is a statistic, that means the more games you make the closer your real profit is to what we have calculated. Playing only once you will win or lose but that benefit will be very different from the calculated, instead by statistics playing many times you will get closer to that number. That’s why the casino already gives you a series of chips for those 20 dollars, so you can play several times with that amount. Because the more you play, the more you let mathematics do its work.

QUESTION: So by playing those 20 dollars from chip to chip I’m going to lose more money?

ANSWER: Not more money but more surely, you will get closer to that number which is negative. But that also makes it harder to win or lose more than that amount. Playing in the long term corrects any positive or negative deviations you may have and brings you closer to the expected value, that means a more stable value, although I remind you that it is negative, so the more you play the harder it will be to win.

QUESTION: Are you telling me that the casino is interested in you playing more times even if it’s the same amount?

ANSWER: That’s exactly what I’m telling you, playing more times will make it harder for luck to benefit you.

QUESTION: So if I want to win I have to put the 20 dollars on one bet?

ANSWER: If you want to opt to win yes, but if you play the 20 dollars to a single bet you are going to win or lose everything, because you only have one bet, If you want to win (or lose) the same amount but playing the chips one by one, you are going to have to win all the times (or lose all the times), because for a same roll a prize of 20 dollars is the same as 4 prizes of 5. But it is not the same to hit (or miss) once, as to hit (or miss) 4 times in a row.

QUESTION: Good but I can also lose more money, because it is also easier to fail 1 time than to fail 4.

ANSWER: If you take risks you can win more or lose more. And the other way you will lose more surely. (statistically speaking)

8. Final Conclusions

it makes no sense to play Roulette to win money.

-The casino doesn’t need to cheat, just the numbers aren’t in your favor

-It’s only possible to win at Roulette if you know some physical phenomenon, or some statistical data of that roulette that can change the probability of some numbers in your favor. . For that you need a study of thousands and thousands of numbers and an acceptable mathematical certainty. In addition, you must write down the appearances of each number in a file, so perhaps this template could help you with this:

 

DOWNLOAD TEMPLATE

 

But beware, if you see that some number comes out more times, the most likely is that it is a product of luck and not that this number is actually more probable. so you will need thousands of prints, and an acceptable statistical certainty. Keep in mind that casinos always fight to randomize their mechanisms as much as possible. But as curiosity you can make a study of many games to see it.

In any case, if you are going to play I recommend you:

• Make only simple and probable bets.
• Be fleeting and make few bets.
• Do not combine bets.
• Limit the money you will play before entering, and never exceed that amount.
• Retire on time (in this last one believe me).

Keep in mind that in the long run:

• The more money you play, the more the house wins.
• The more you combine, the more the house wins.
• The more you play, the more you are sure and the more the house wins.

So the casino always wins?

It doesn’t always win, but if you go back it will end up winning.

Remember that the game never ends.

If you want to see more videos like Poker or Blackjack you can visit my math for all channel where I study them in detail.