The Mathematics of Poker – Range, Position and EV
NOTICE: This article does not intend to promote gambling or ludopathy. It is an analysis focused on the mathematics of gambling, where it is explained whether gambling can be profitable or not and how to analyze it.
In this video I analyze other more technical aspects of Poker such as range, position or EV calculation.
1.Range
2.Poker Factors
3.Position
4.Poker EV
4.1.Call EV
4.1.1.Call EV calculator
4.2.All-in EV
5.Other Factors
6.Heads up Strategy
7.Nash Equilibrium
In the last poker math video we saw a summary of the rules of the game, and what the probability of linking each hand is.
We then looked at the outs and odds, which are the probabilities used in poker, and learned how to calculate them and refer to our table of odds and outs.
We also saw how we can approximate these values mentally without the need for tables, and finally we learned how to use a poker calculator, and saw how the odds we calculate for our projects relate to our real probabilities.
In any case, I didn’t answer how to calculate our odds when we don’t know the cards of our opponents, and neither because a hand that has little chance of being tied can be profitable. That’s why if you were left with the doubt or are simply curious to answer these questions we go with the second part of the poker math.
1.Range
As we saw in the previous video, Poker is a game of incomplete information, since we do not know the cards of our rivals. Consequently what we can calculate comes from an estimation of what hands they might have, based on the projects they can complete with the community cards. But also knowing which hands they usually play frequently or which ones they prefer to discard in certain phases of the game.
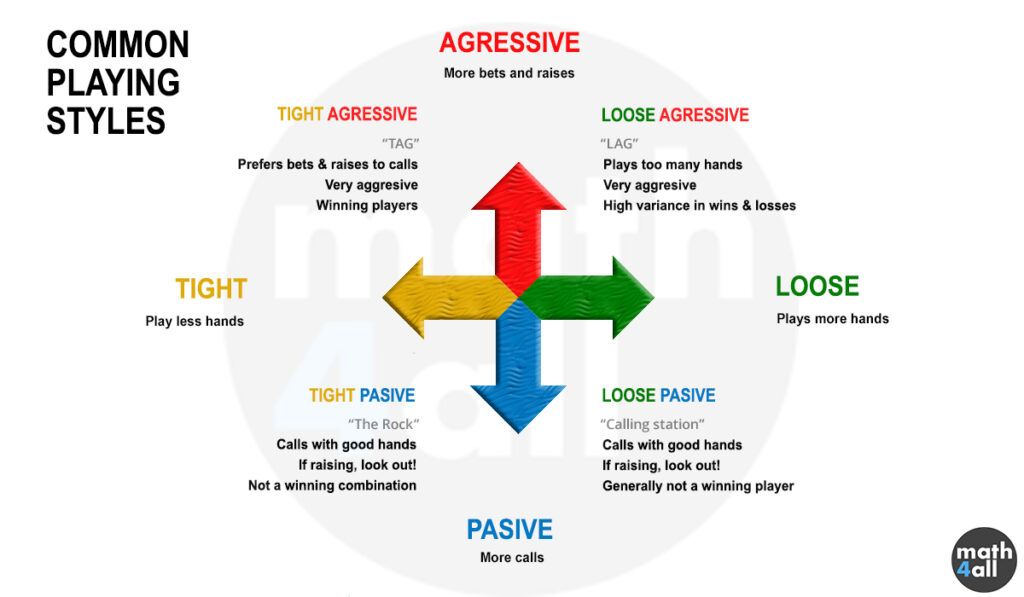
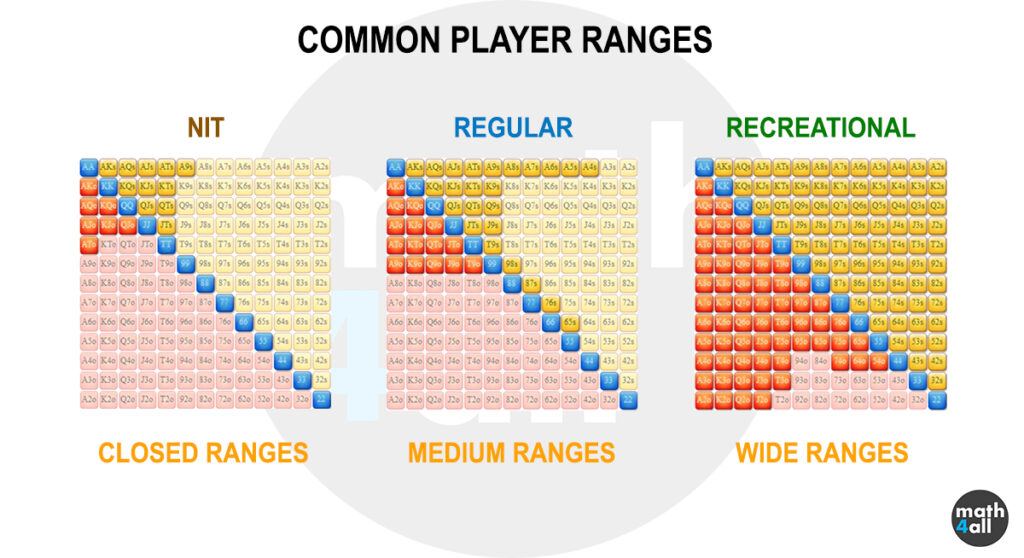
Some players tend to play a very small number of hands, because they feel safer playing like this. Others, more recreational, prefer to use a larger number. Have you ever wondered what kind of player you are?
The reality is that we all have a filter to choose which hands we play and which we don’t, which is more or less big depending on our style of play.
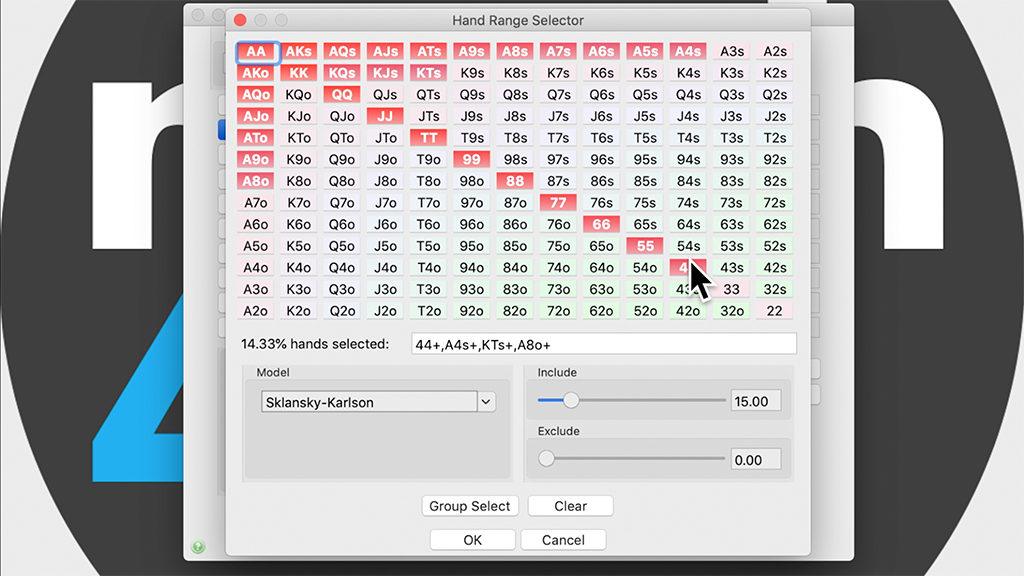
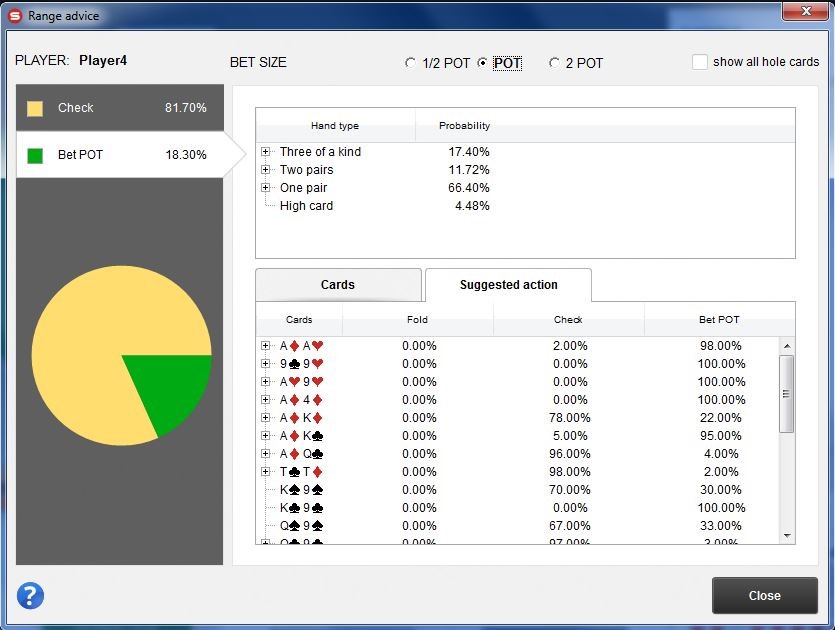
Well, the group of cards that make up that estimate is known as range and is represented at the software level with a matrix where you can select which cards make it up.
If you want to calculate your hands probability taking it into account, what you should do is calculate the probabilities of your cards against that range you estimate, eliminating all those hands that are impossible or very unlikely that the opponent is playing, given his profile or the game situation. This way you will get a calculation as close as possible to the real one with the information you have. That’s why the better the estimation you make, the more accurate will be the calculation of your probability, and that’s why it’s important to acquire a technical knowledge about what ranks our opponents may have. But it is also important to know our own rank.
On a practical level, I recommend you a Tracker Software to do this, because besides calculating probabilities with ranks it is able to analyze the game of your opponents and offer you personalized statistics. It does this by saving the data of the games you are playing and in this way you can know what number of hands you play voluntarily, the percentage of times you have increased in the preflop, or any variable you consider important. A player’s statistics can always give us a long term advantage in making decisions. Although keep in mind that this is only for Online Poker.
The truth is that this software is very, very cool. And now that you’ve seen how to calculate ranks, what else do you think you should take into account to make a decision?
2.Poker Factors
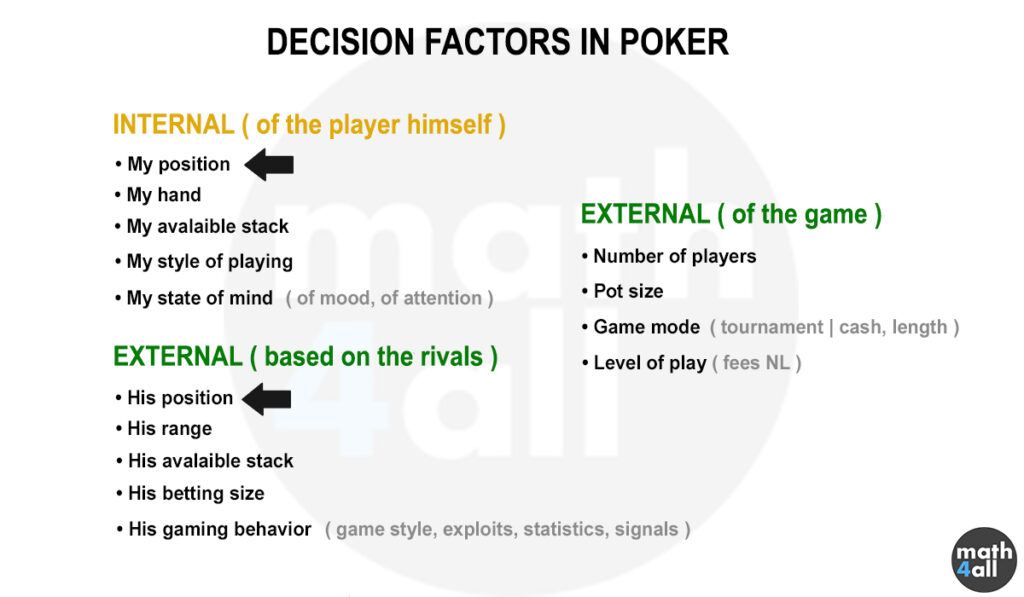
Deciding when to match a bet, raise it with a certain amount or throw away our cards is what determines how good players we are in the long run, but choosing one or the other depends on many factors, so I have made a list for you to look at:
Some rely solely on our information, and others rely on information provided to us by our competitors. But then there are others that depend solely on the game such as the number of players. The more players there are at a table, the more likely it is that one of them will have a stronger hand than ours, as we face more players on average per round. That is why we must adapt our game with a more exclusive range, and also reduce the range we estimate of our opponents, because it is less likely to win with the same hand when there are more possible better hands.
3.Position
As we see there are a lot of factors, but not all of them have the same importance.
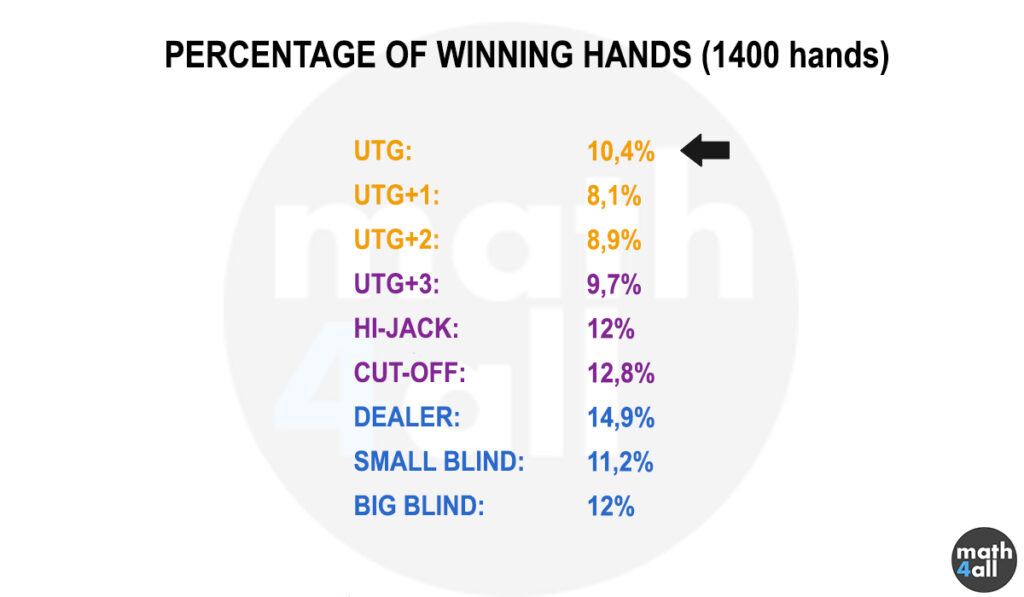
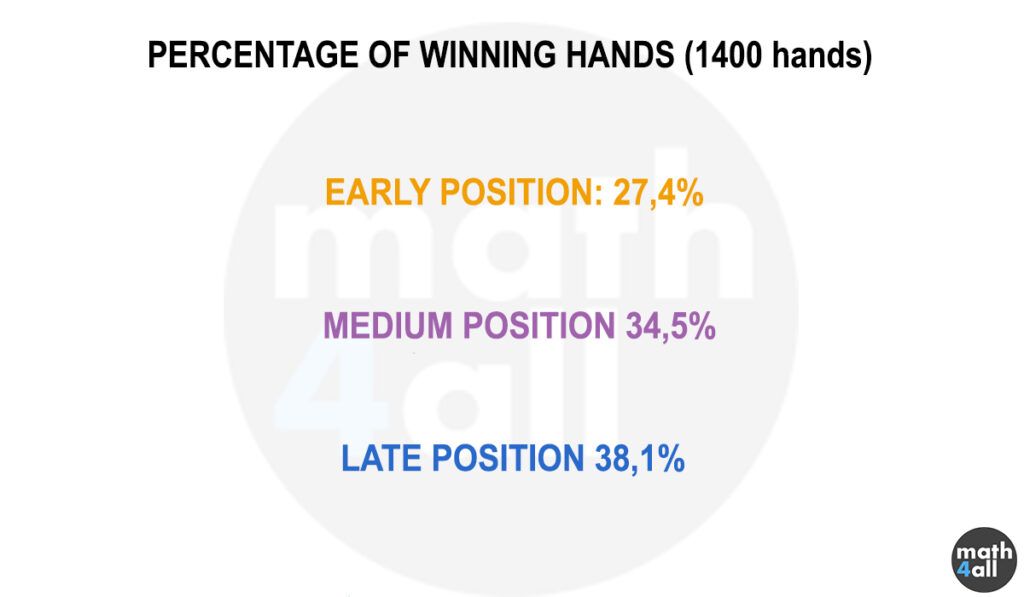
One of the factors considered most important in poker is the position, as it can be used to get extra information from your opponents, or also to lie. If you play in an early position, you have no information about what your opponents are going to do, and since you can’t discard any player you are forced to play a shorter range of hands. On the other hand, if you play in a late position, you get information about the bets that are made or the players that withdraw, so you have certain information that can give you an advantage and more chances to win. That makes each player adopt a different game and range depending on their position and that logically offers different results. But how much of different? Well, 9 players in over 1000 hands have been analyzed to see which position has the most advantage, and this is what has been observed:
As we had already deduced the last positions are usually the ones that offer us more profit, but curiously and against what I had said, the first position also has a quite high percentage of victories. This is explained by the fact that many players use early positions to bet or raise as if they had a strong hand, whether they have it or not.
If we make a summary, we can see that a late position is the one that benefits you the most, but the early position can also serve to bluff you.
Playing good poker doesn’t seem to be easy, you have to be good enough to overcome the losses of the game and even losses on commissions. And with all these factors our decisions depend on many things. So, is there any mathematical formula to decide what action we take?
4.Poker EV
Although position is a very important factor, its influence decreases as fewer players are left, since by reducing the number of rivals we can consequently steal fewer chips. So when there are only 2 players left at the table, which is usually the case, the position is no longer a factor to take into account and we can establish a mathematical method to know what decision we should take, based only on the size of the pot, the size of the bets and our probabilities.
For that a new concept is defined called EV that comes from (Expected value) and is based on the concept of long term gain. To know if a play suits you or not, the most intelligent thing is to calculate what average gain we would obtain if we repeated many times that same play. And that is precisely what calculates the EV, subtracting the probability of winning by the profit less the probability of losing by the loss. In this way you can know that profitability has for example to equal a bet.
4.1.Call EV
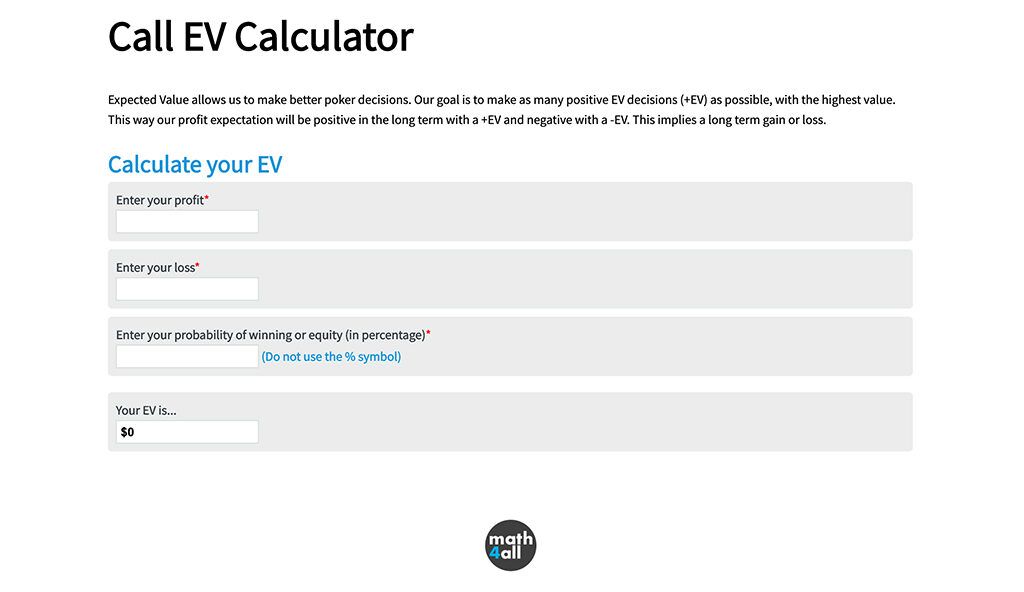
When the EV is negative, equalizing or making a call is not profitable, but if it is positive, it is a priori profitable in the long term as it is higher than the EV of folding, which is 0. Note that it is also possible to have a positive EV even though you are more likely to lose, if the benefit outweighs the risk. Since it can be more profitable to win few times with much money, than many times with little money. This answers the question of why it can be convenient to bet with a small probability. I have included this EV call calculator in case you are interested in calculating the expected value of your possible call.
To calculate the EV mentally you can use the known pot odds, which are no more than the proportion between what we win against the bet we have to make, and which are compared with the odds (which are the times we lose for each time we win). As both are calculated with the same proportion, you only have to compare odds and pot odds to know if it is profitable to go to a raise or not, so this is a practical way to calculate the EV for the live game.
4.2.All-In EV
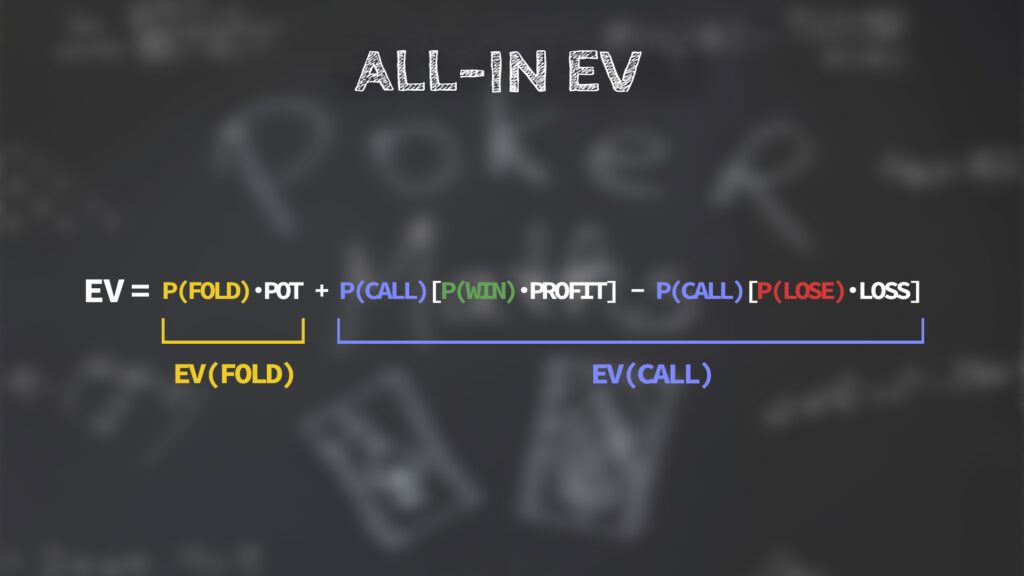
To know instead if doing an all-in is profitable, the thing changes, since it is important to take into account the response of our rival, which can be to go or to fold based on the amount that we bet, so the EV in this case also includes the estimated probability that one action or the other happens, and can be calculated in this way.
Which is basically the Fold EV plus the Call EV
There are many formulas to determine our actions, such as the minimum bet you have to make to remove the odds necessary to the rival to pursue their project and many others that you can search on the Internet:
AM = (Outs x P)/(50 – 2 x Outs)
5.Other factors
The truth is that although these formulas are useful, there are other factors that can also influence when making a decision:
-One of them is the confrontation cost. If you have a profitable move but few chips and you don’t have the possibility of re-buying or you simply play in the short term, it may not be smart to match or to do all-in if doing so may have a confrontation cost of losing all or a large amount of chips, compared to not confronting (especially when our probability of winning is low), so in modalities such as tournament, it is also important to evaluate our decisions based on the chips we have and those of our rivals. A mathematical model that takes this into account is the ICM model, which is used especially for the bubble phase of tournaments.
-Another factor considered the most important to change those decisions is the knowledge of your rivals, which can serve to adapt and exploit their meta-game as much as possible, increasing or decreasing the bet size, the amount we have to pay to certain rivals, or simply to avoid or encourage certain clashes, which can give us an advantage.
It doesn’t seem easy to decide with so many things, so the experience also plays a fundamental role to be a good player, although are we really able to learn all the situations of Poker?
6.Heads up Strategy
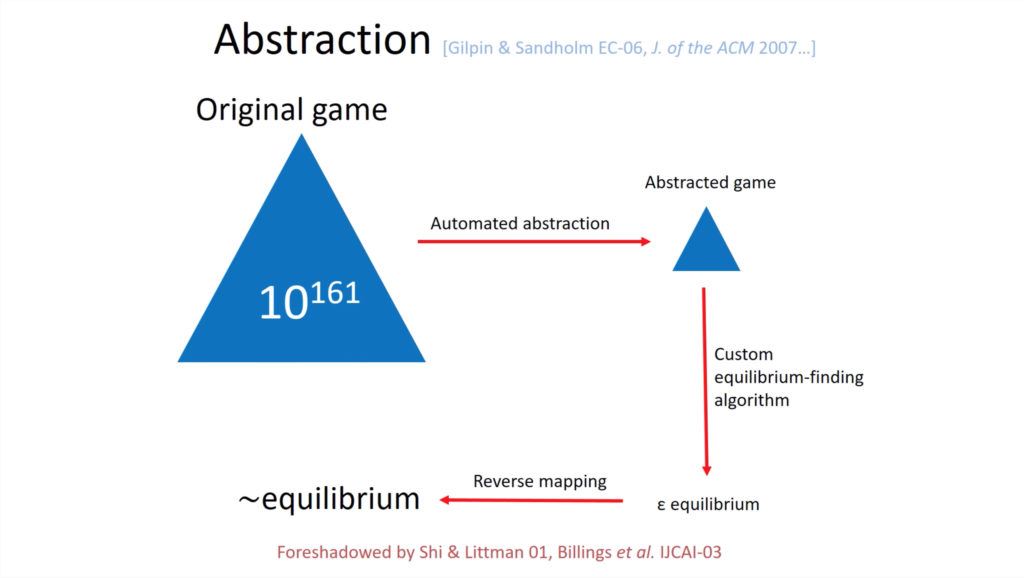
Only in the Texas Holdem for 2 players there are 10^161 different decisions possible, which is more than all the atoms that form the universe. This makes it impossible for a human to learn which is the most advantageous decision for all that immensity of situations. Although, as you have surely thought, there are programs where you can consult how to act in most of the possible cases to improve your strategy. These process millions of hands based on exploiting themselves, and offer us the most profitable actions at the statistical level, which you can use to adapt to your game and exploit your opponents, so currently to be a good player is also important to know how to interpret statistical data correctly.
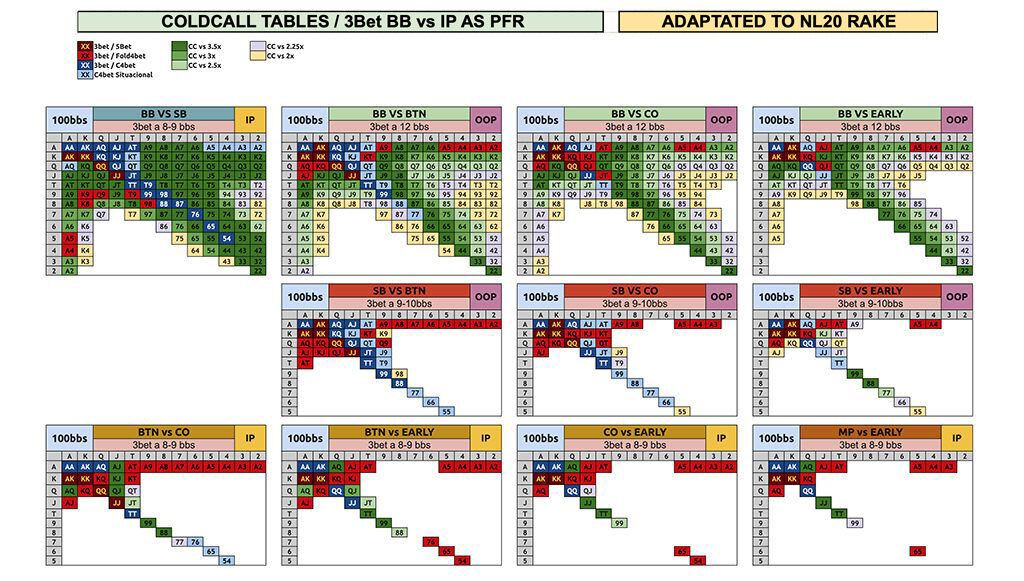
One of the most important decisions that we must take in Poker is how to play our hand in the heads up, since that conditions us a lot during the following betting rounds, that’s why it’s important to have a previous well defined strategy that you can consult. That’s why I have included a series of tables based on the study of these programs made by a professional player (Zeros) and that could be helpful if you have them at hand during the game. In them you have the action plan based on the optimal return for any particular situation in the heads up, which can be very useful for online poker, so if you are interested, you have a link in the description, along with the link to these programs that I have commented in case you want to consult another situation. (And it’s not that I want you to play Poker but if you do, do it well).
Now that you have seen that Poker is a very mathematical game, the most important question of all arises, is it possible to play Poker in a perfect way? Let’s see it:
7.Nash Equilibrium
In 1951 a certain John Forbes Nash better known as John Nash elaborated a doctoral thesis demonstrating that any game with a finite number of mixed strategies has at least a Nash equilibrium. This balance is given when all the players have chosen in the best possible way and none of them can improve their strategy by much change it, as long as the others maintain theirs. This balance ensures that in a zero-sum game like poker, we will never lose in the long run.
How is this possible?
The search for this balance is not simple, because we must find an optimal combination that satisfies all players among many possible, which added to the amount of decisions that can be made makes it a computer challenge. Finding a balance in the heads up is less difficult but in the River it is much more complicated. (To understand this, try to imagine all the situations that can occur in this phase of the game)
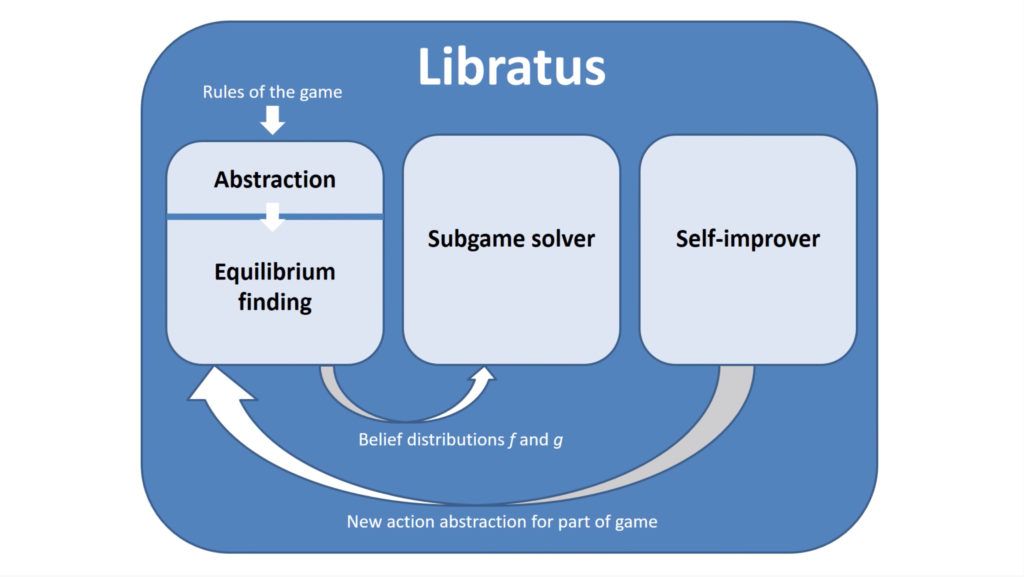
As there are so many possible casuistry, it’s too expensive to compute a strategy for each hand or bet size, so scientists have chosen to abstract the full game to a more simplified version in terms of values and bet sizes, which allows the search for balance more efficiently, and that approximates in a very precise way to the full game through a set of algorithms. Using intelligently the calculation of this balance, they have built an artificial intelligence that plays poker for two players in a practically perfect way.
In 2017 the Libratus software managed to beat the best world professional poker players for the first time with a significant statistical advantage, which is a historical fact for games of incomplete information. And all this thanks to mathematics.
Luckily or unfortunately Nash’s equilibrium is only possible for 2 players, since it is possible to lose in long term expectation in Poker of 3 players or more, especially if one group of them gets together to eliminate another. Even if a balance is calculated for all three players, that combination does not have to be a Nash balance in itself. Consequently, if you play online poker with more than two people, you don’t have to worry for the moment, because their future is assured, although, who knows until when?