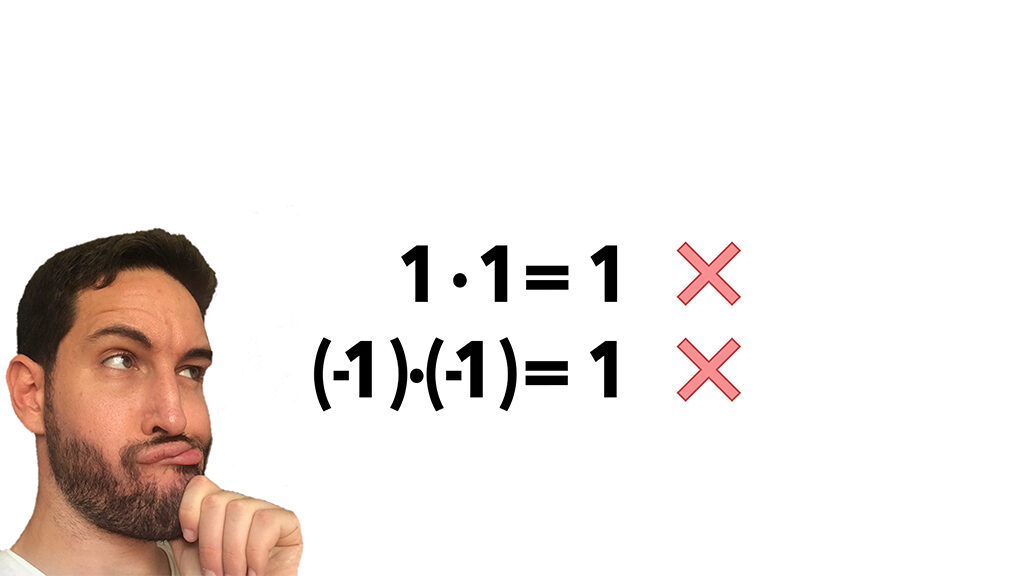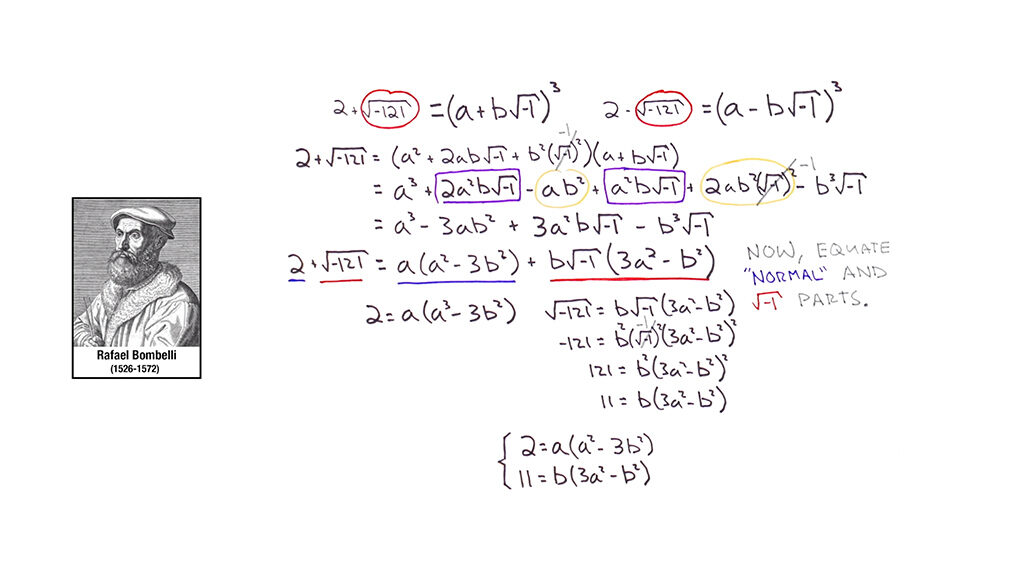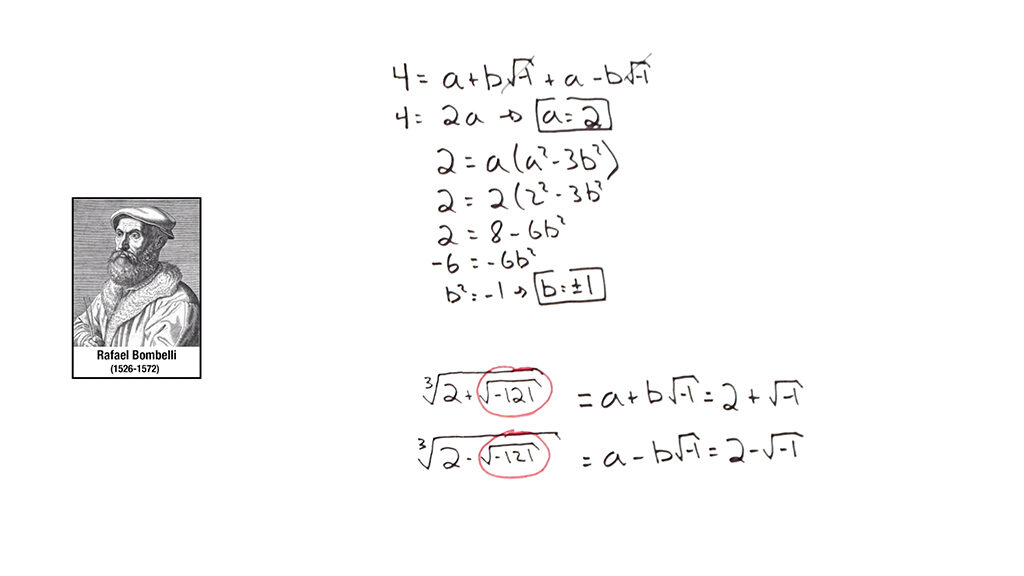Los Números Complejos
1.Historia de los Conjuntos Numéricos
2.Descubriendo la Raiz de -1
3.El Número Imaginario i
4.Situación
5.Representación
6.Operaciones
7.Calculadora de Números complejos
8.Historia de los Números Complejos
¿Alguna vez te has preguntado si los números que utilizas sirven para todo? ¿puedes hacer cualquier cosa con ellos o tienen sus limitaciones?
Si quieres que te lo cuente, no te pierdas el sorprendente mundo de los números complejos.
1.Historia de los Conjuntos Numéricos
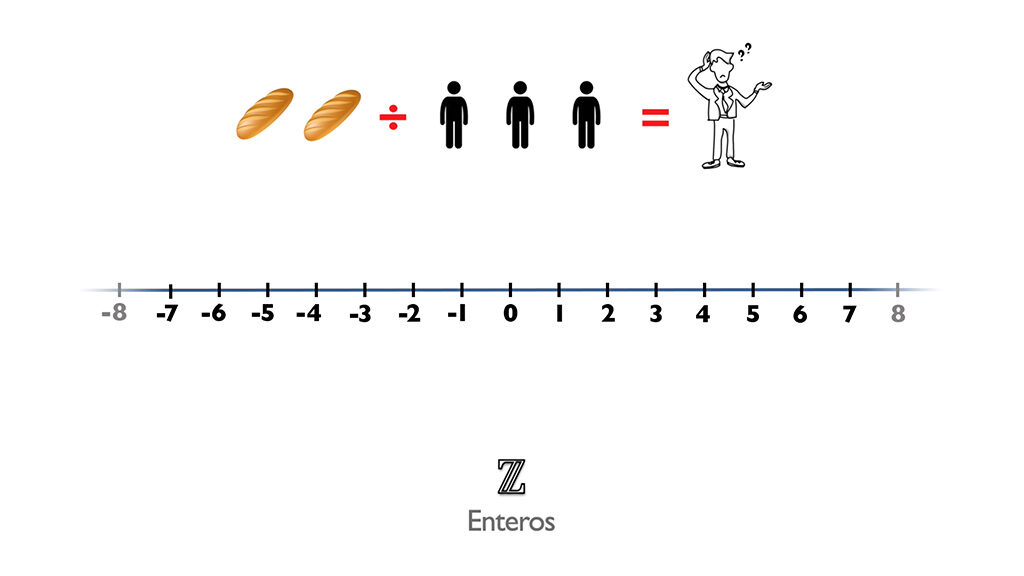
Los números que utilizas no han sido siempre los mismos. Al igual que aprendes primero contar, después números negativos, luego fracciones y vas ampliando… la historia de los números ha tenido exactamente la misma evolución.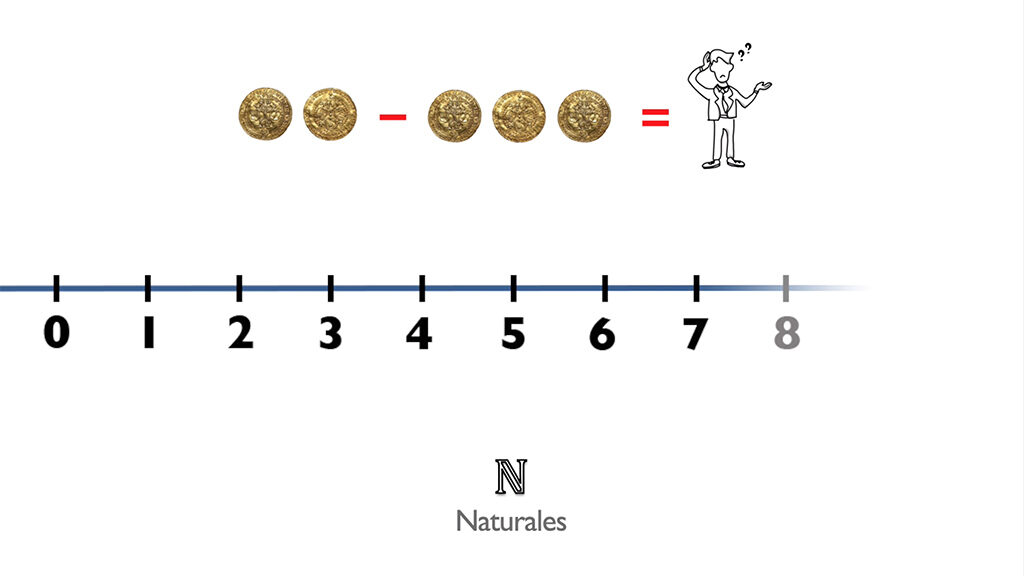
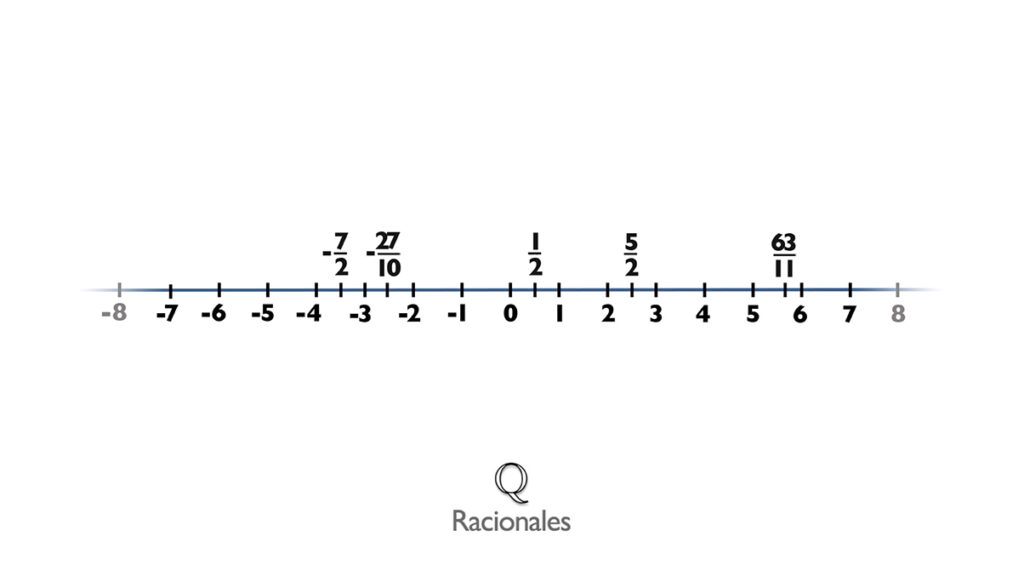
Los números naturales (N) que usábamos para contar no servían poder representar deudas o resultados negativos, así que tuvieron que ampliarse a los números enteros.
Pero los enteros (Z) no eran muy completos, porque tampoco servían para poder repartir porciones o calcular las partes de un todo. Por eso tuvieron que ampliarse nuevamente a los racionales (Q).
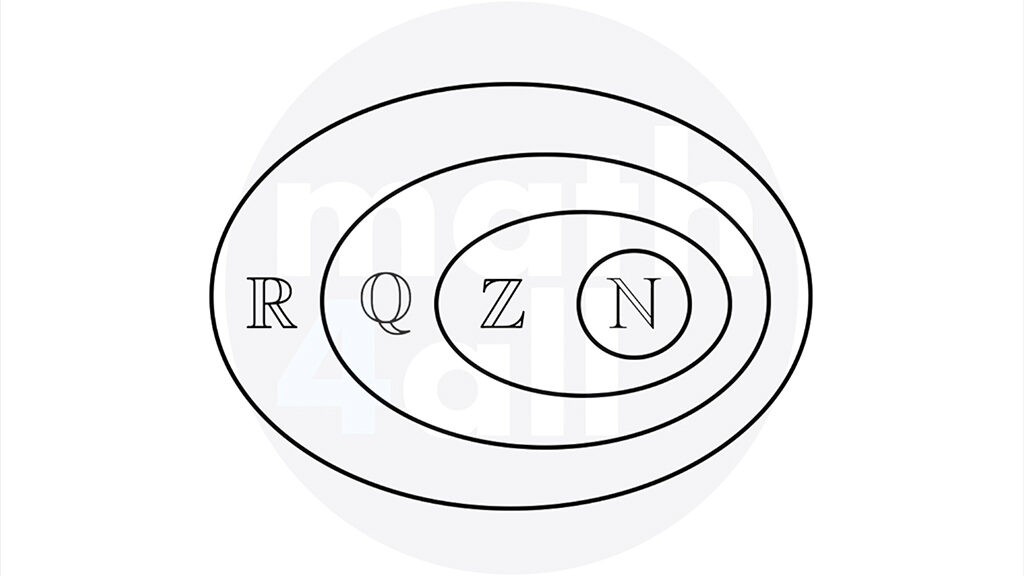
Después se añadieron los irracionales (I) que no pueden expresarse como una fracción entera, y de esta manera ya teníamos los números reales, un conjunto para albergarlos y operarlos a todos.
2.Descubriendo la raiz de -1
Pero.. ¿seguro que todos? ¿Y si te dijera hay mas números que los reales?
Mira esta ecuación:
X² + 1 = 0
Es una ecuación de segundo grado aparentemente sencilla, y basándonos en el teorema fundamental del Álgebra tiene 2 soluciones porque es de grado 2.
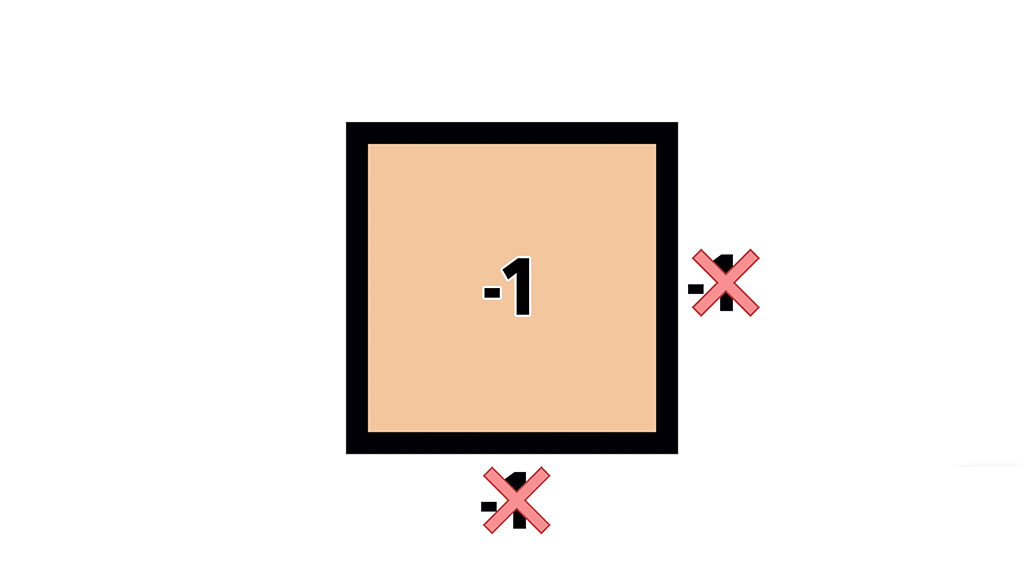
Si la operamos y despejamos la x, las dos soluciones de x son raiz cuadrada de un número negativo. La cual no tiene solución porque no podemos multiplicar dos veces un número y que dé negativo.
Si multiplicamos 1 dos veces nos da positivo y si lo hacemos con -1 también nos da positivo. Dicho de otro modo no podemos elevar un número real al cuadrado y que nos dé -1, porque eso sería como pedirle a un cuadrado de área -1, que los dos lados sean iguales cuando solo tenemos 2 combinaciones y ninguna sirve.
¿Entonces cómo puede ser que haya 2 soluciones?
¿Nos conformamos con que no existen o aceptamos esas soluciones no pueden ser números reales?
Ya sabes que un matemático nunca se rinde!!! pero como conseguimos que x² sea -1?
Tenemos que multiplicar dos veces el mismo número y llegar hasta -1…. pero ¿no parece posible verdad?
3.El número imaginario “i”
Sabemos que multiplicar por -1 es como cambiar de signo. Ya que saltamos de ese número a su inverso en la recta real. Si tenemos el 5 pues acabamos en -5 y si empezamos en -5 acabamos de nuevo en 5.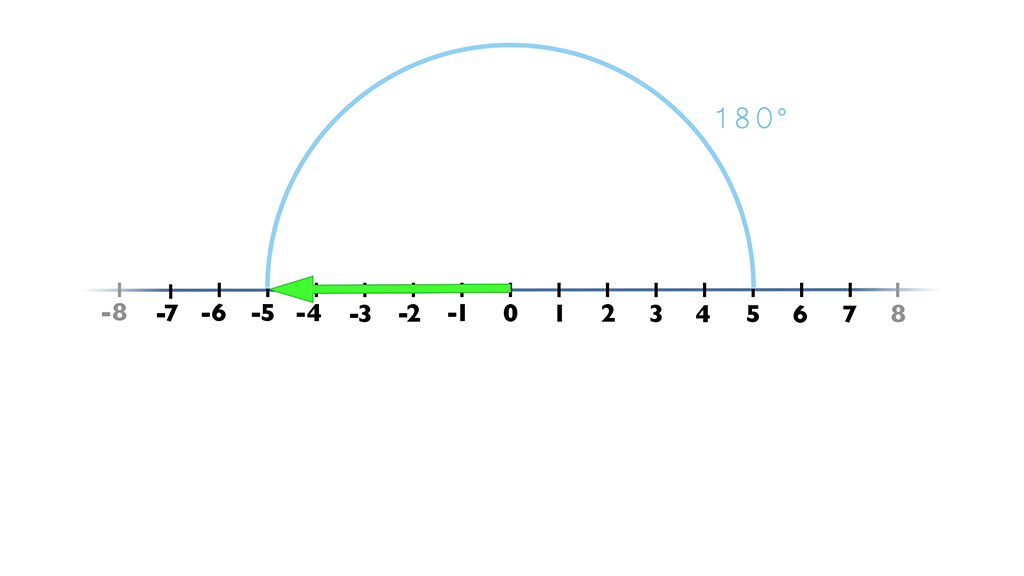
Pero entendámoslo de una manera visual. Si representamos el número como un vector, multiplicar por -1, es cambiar la dirección de ese vector a la contraria para calcular el resultado. O dicho más sencillo rotar 180 grados desde el origen. Si en vez de multiplicar una vez, lo hacemos 2 volvemos al punto de partida, porque rotamos 2 veces 180 y eso es una vuelta entera.
Por eso no podemos llegar a -1 multiplicando 2 veces el mismo número!!!
O quizá si?
¿Que pasaría si cada multiplicación recorriera solo la mitad del camino?,
en ese caso el número tendría que estar en el punto intermedio entre 1 y menos 1, pero el único número que hay es el 0, y sabemos que 0 no puede ser porque al multiplicar una segunda vez se quedaría de nuevo en 0. Entonces, sabemos que ese número tiene que estar a la misma distancia que 0, pero no puede ser 0. Con lo cual solo cabe una posibilidad y es que el número esté obligatoriamente fuera de la recta, ya que es la única manera de que el vector rote 90 grados en lugar de 180.
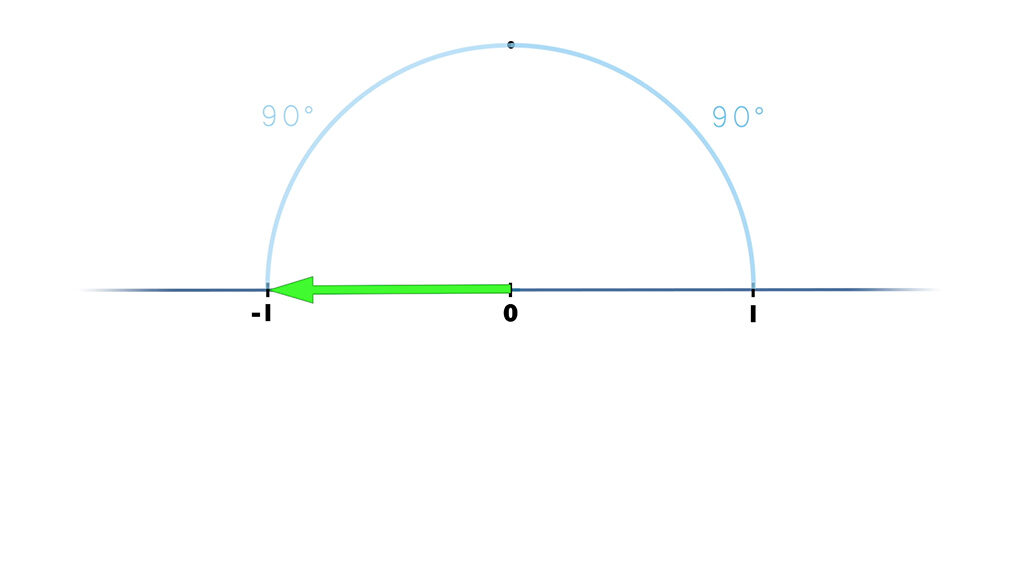
Eso quiere decir que el número que estamos buscando está situado lateralmente en una segunda dimensión con respecto a los números que conocemos!!.
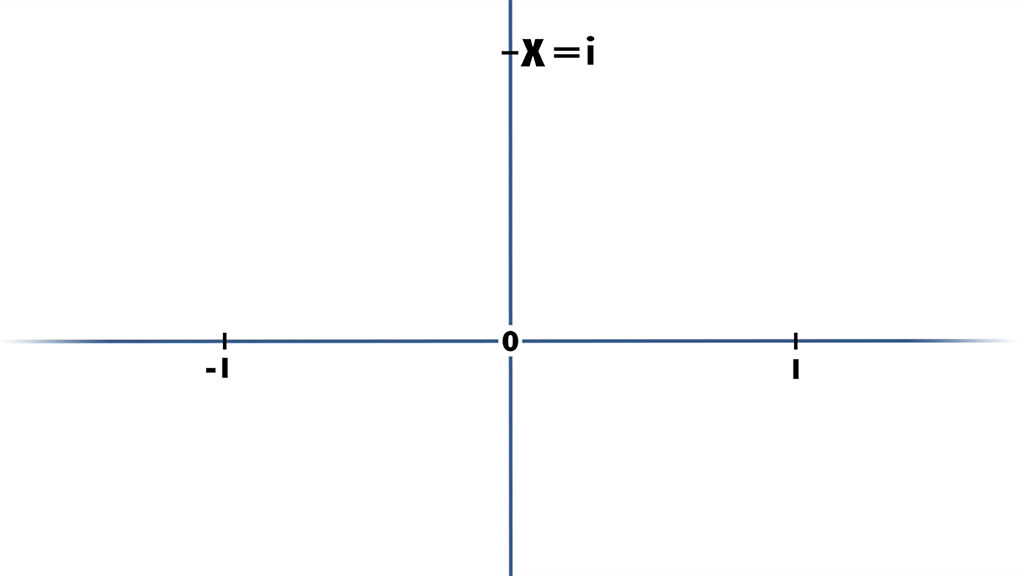
Pues bien a este número se le conoce como número imaginario “i” (aunque no me gusta mucho llamarlo así), y es la primera unidad para el nuevo eje de ordenadas, que lógicamente podemos representar como (0,1). Abscisa 0 y ordenada 1.
¿Como íbamos a encontrar la solución viendo los números como puntos de una recta?
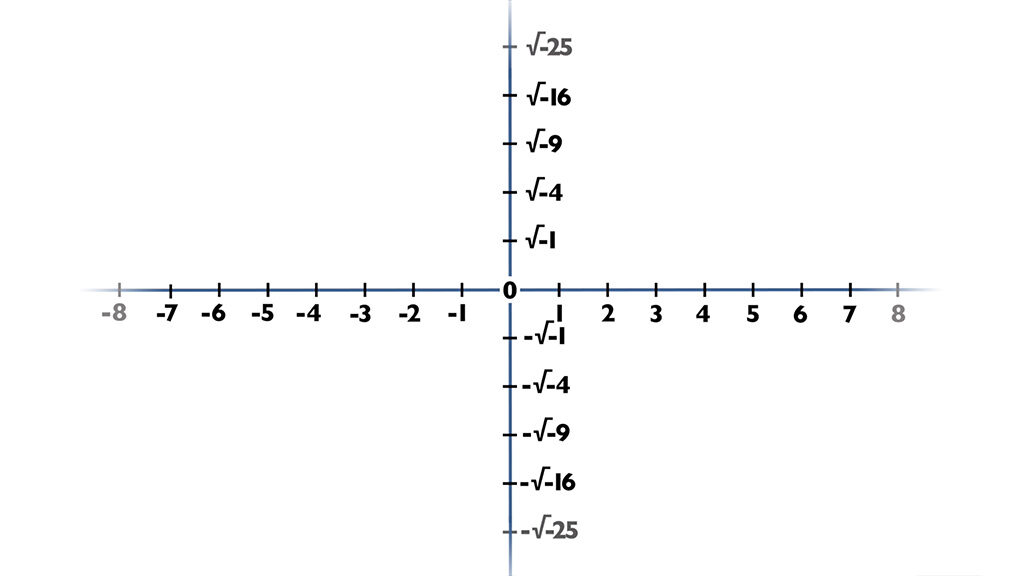
Ahora ya puedes situar espacialmente cualquier raíz cuadrada negativa, y sus respectivas inversas, ya que si recuerdas la ecuación existían dos soluciones y nosotros sacamos tan solo la primera de ellas rotando el vector en un sentido. Pero también podíamos llegar a -1 rotando 90 grados en sentido contrario multiplicando por -i dos veces. Evidente ¿o no?.
4.Situación de los Números Complejos
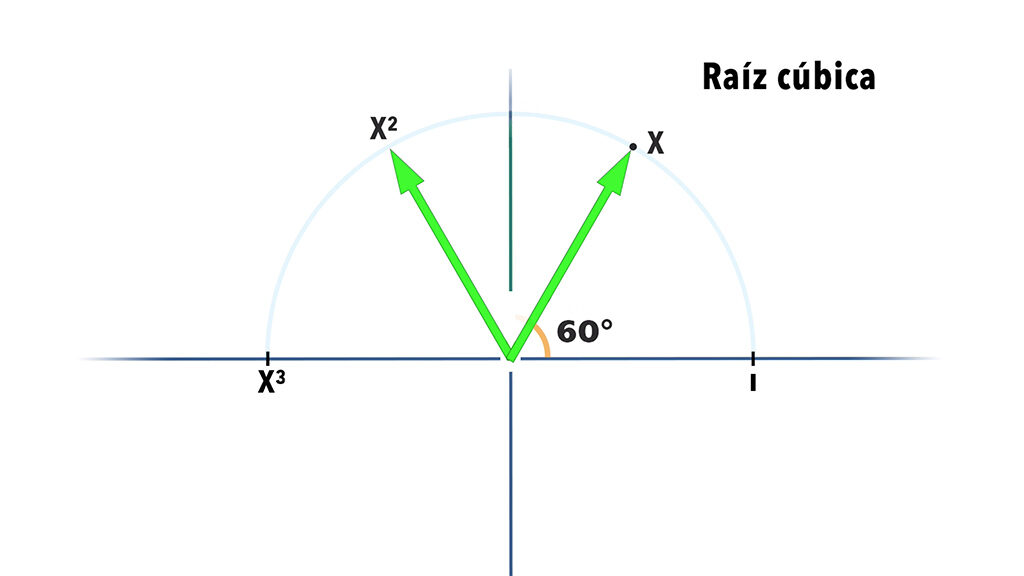
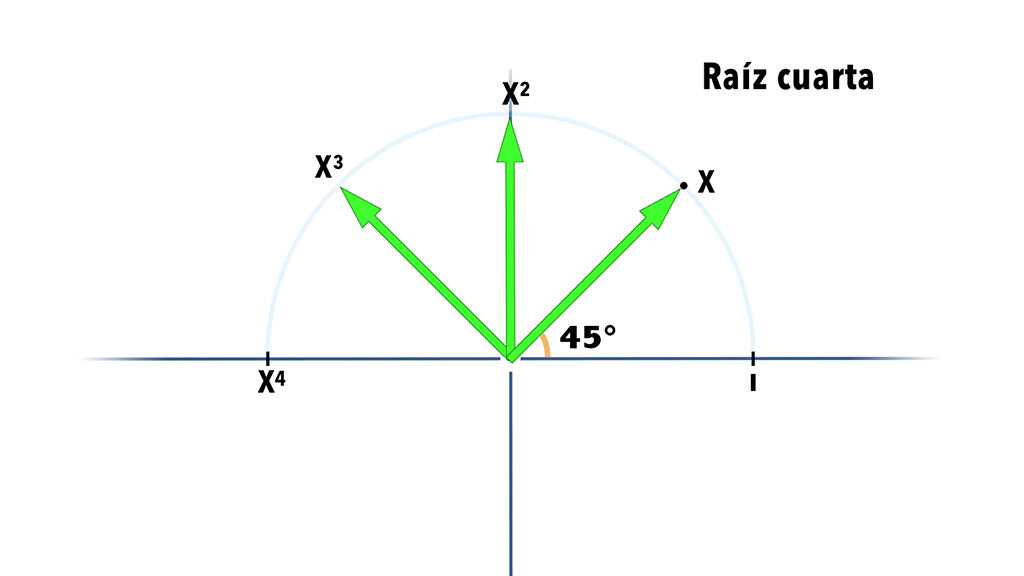
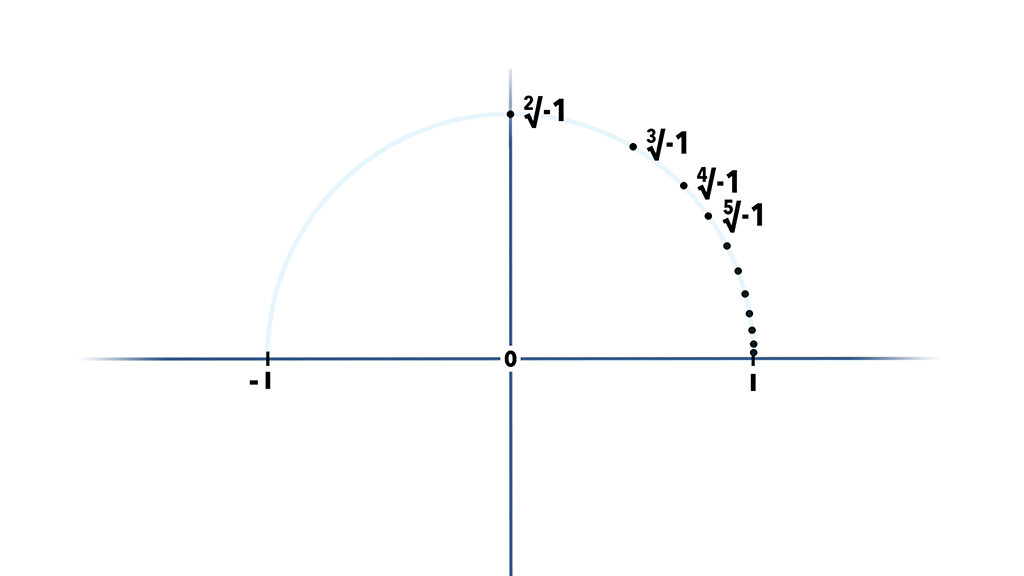
Ahora ya sabemos que hay números perpendiculares o laterales a los números reales!, pero estos tampoco son todos… Si en vez multiplicar 2 veces buscamos multiplicar 3, necesitamos un ángulo de 60 grados en lugar de 90, y son 4 de 45,
con lo cual todas estas raíces se sitúan espacialmente fuera de los ejes, lo que significa que hay números por todo el espacio!!!!
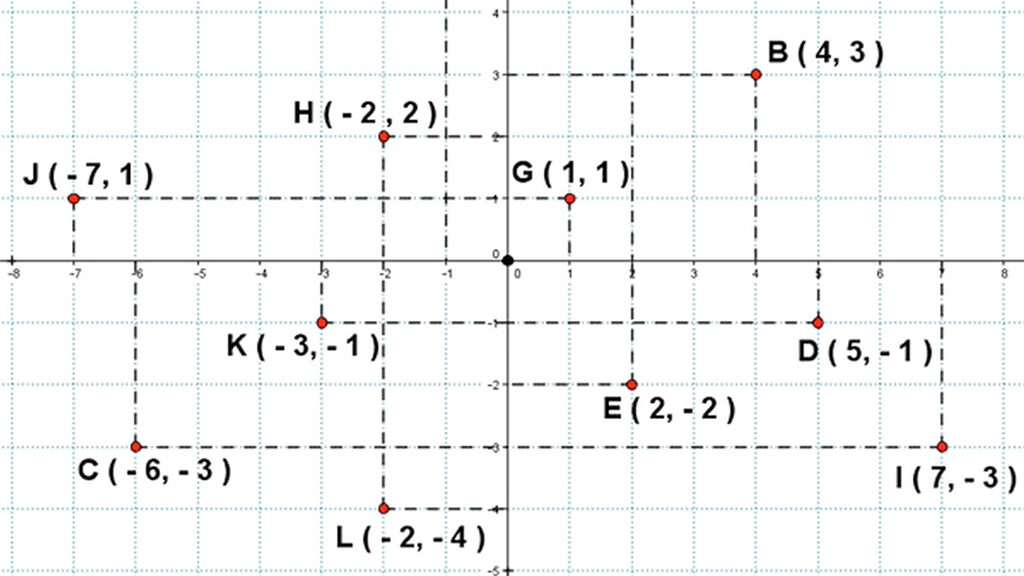
Si los números están en cualquier parte del plano, lo correcto es expresarlos en dos dimensiones, ¿o no?
Pues ese es precisamente el conjunto de los números complejos, los cuales podemos representar con una simple coordenada.
Pensábamos que solo había una recta, ahora resulta tenemos un espacio lleno de números!!! Vaya locura!!
5.Representación de los Números Complejos
Aunque no es necesario expresarlos siempre con coordenadas…
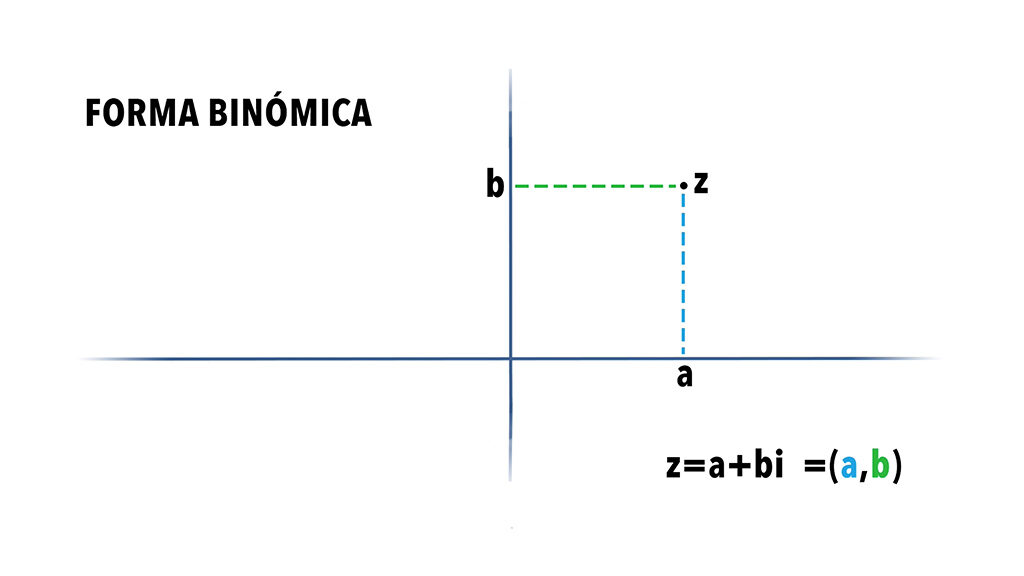
-La representación de un complejo mediante un par ordenado, es solo la forma binómica.
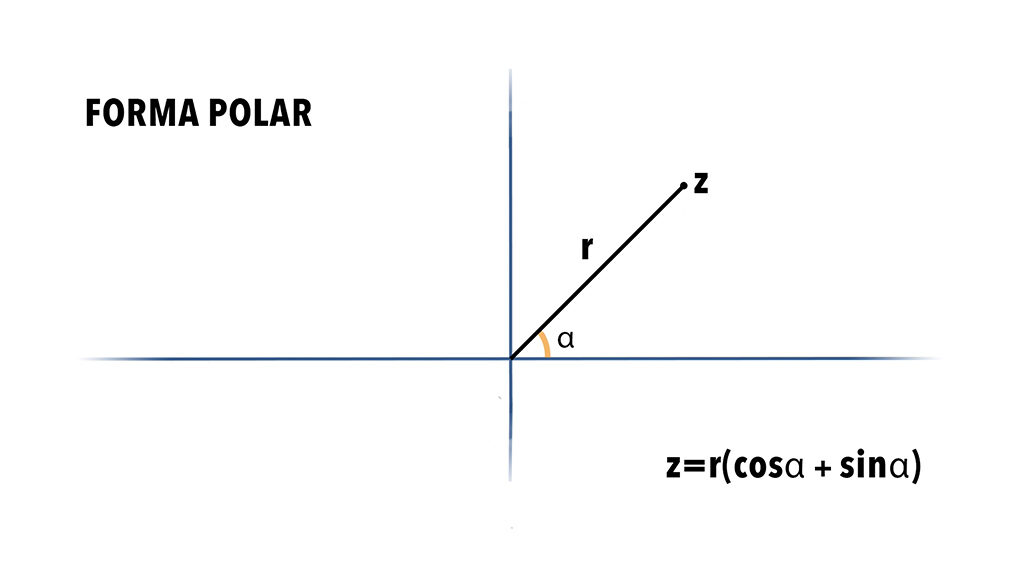
-Pero si lo hacemos con un vector y un ángulo, tenemos la forma polar o trigonométrica (y pones la fórmula con el modulo y el argumento)
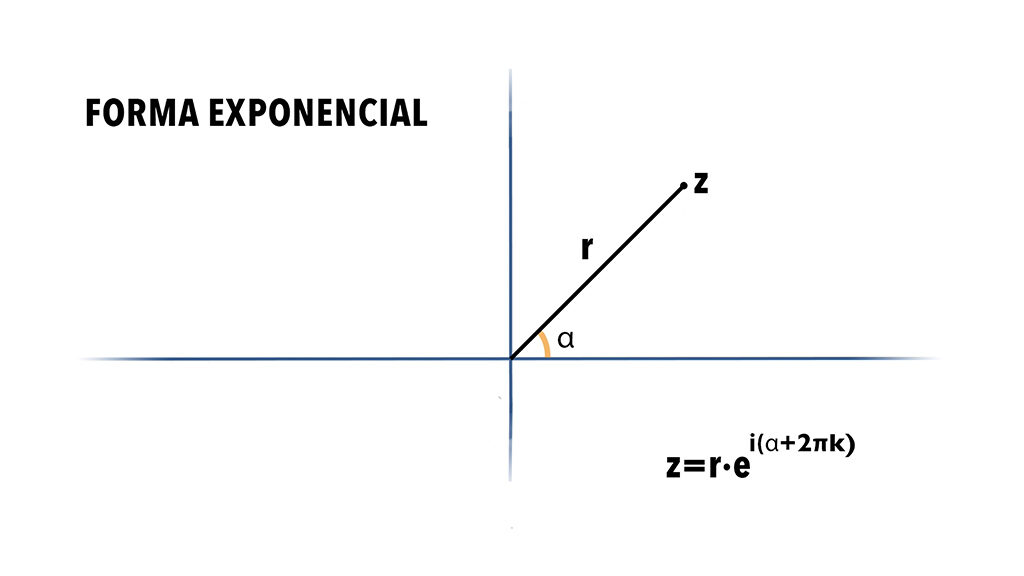
-Y si lo hacemos como una potencia ( que nos lo permite la Identidad de Euler ). Tenemos la forma exponencial.
Elegir una u otra notación depende de cuál nos sea más sencilla para trabajar con las operaciones que tenemos que hacer.
6. Operaciones de Números complejos
Pero imagino que te preguntas ¿como demonios se operan números en dimensiones?
Estas son las operaciones:
SUMA: (a,b)+(c,d)=(a+c,b+d) Pues bien, la suma de complejos es muy sencilla. Parte real con parte real, y parte imaginaria con parte imaginaria. No podemos mezclar ambas cosas.
PRODUCTO: (a,b)x(c,d)=(ac-bd,ad+bc) En cambio el producto si cruza ambas componentes, para poder cumplir las reglas geométricas que hemos visto. Aunque se puede calcular fácil con la propiedad distributiva y teniendo en cuenta que i² es -1.
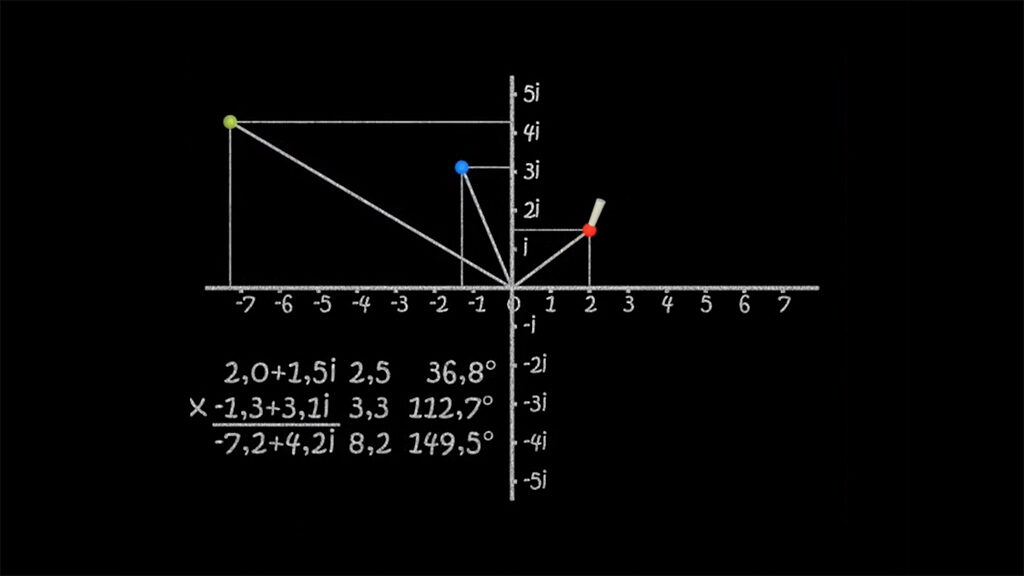
En definitiva si interpretamos el producto geométricamente:
-Es muy fácil ver que los módulos o distancias de los vectores de los dos números se multiplican y que los argumentos o ángulos se suman. Esto es suficiente para deducir que:
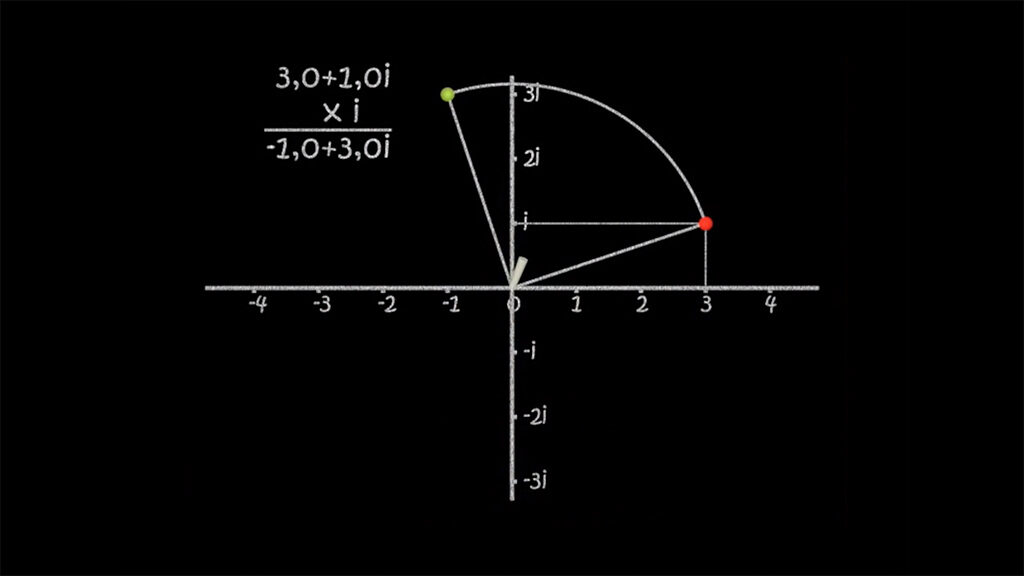
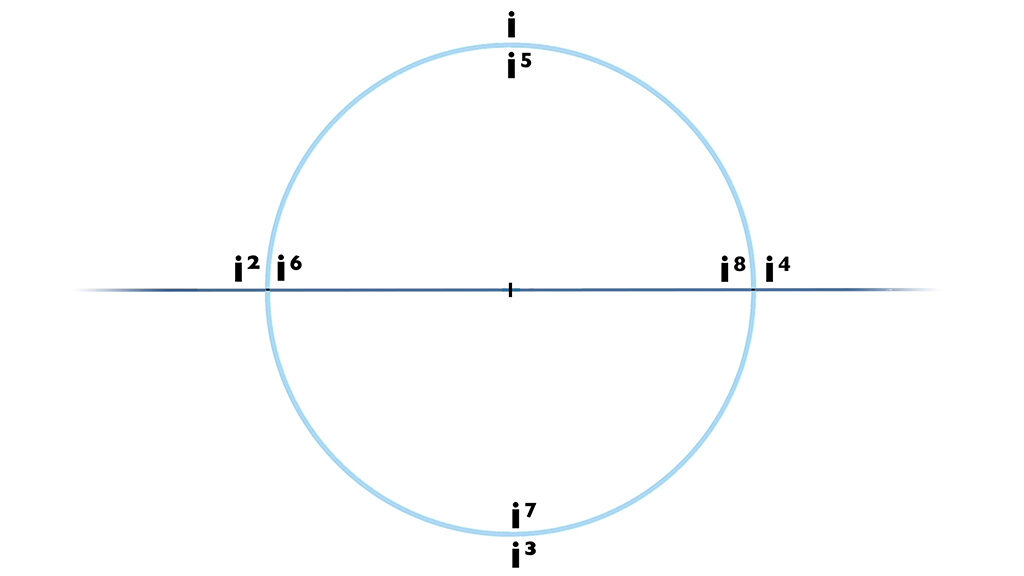
-Multiplicar un número real por un numero imaginario (puro) positivo es rotar 90 grados, y si es negativo -90 grados. (Con lo cual si i² era dar media vuelta i a la cuarta será dar la vuelta completa y volver a 1, y cualquier potencia posterior se repite).
-Que el producto de un numero real por un imaginario puro es imaginario puro.
-y por último la más impactante, que el producto de dos imaginarios puros es siempre real!!!.
(fíjate cualquier punto en abcisas al que apliques esos ángulos acabará en ordenadas, y viceversa)
¿Curioso verdad?, números que pensabas que no existían pueden darnos un resultado que si existe. Parece que ni los reales son tan reales ni los imaginarios tan imaginarios!!
Como ves todas estas operaciones amplían lo que ya conoces pero en números complejos, aunque también puedes sumar o multiplicar 2 números convencionales, que tienen segunda componente 0, y el resultado será el mismo.
Ahora si que ya podemos hacer lo que queramos!!
Lo primero que teníamos pendiente era comprobar que i² es -1:
y como ves si aplicamos la regla del producto todo cuadra.
7.Calculadora de Números Complejos
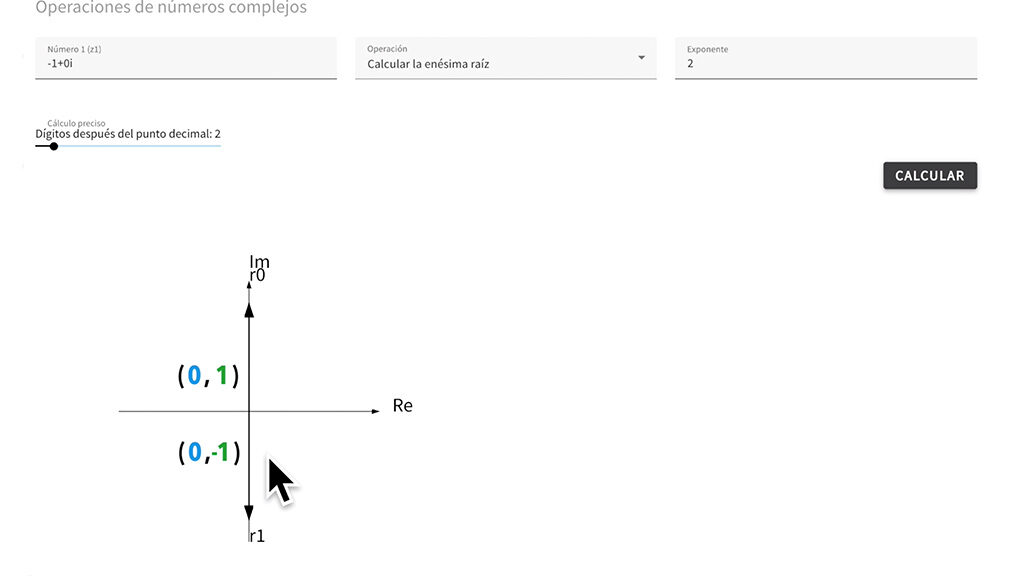
Pero también teníamos pendiente comprobar las dos soluciones de raíz cuadrada de -1, por eso vamos a usar nuestra calculadora de números complejos, seleccionamos la operación raíz cuadrada y como ves también es así (0,1) o (0,-1)
IR A LA CALCULADORA DE NÚMEROS COMPLEJOS
¿Ves como existían las soluciones?, la clave era entender los números como algo en dos dimensiones.
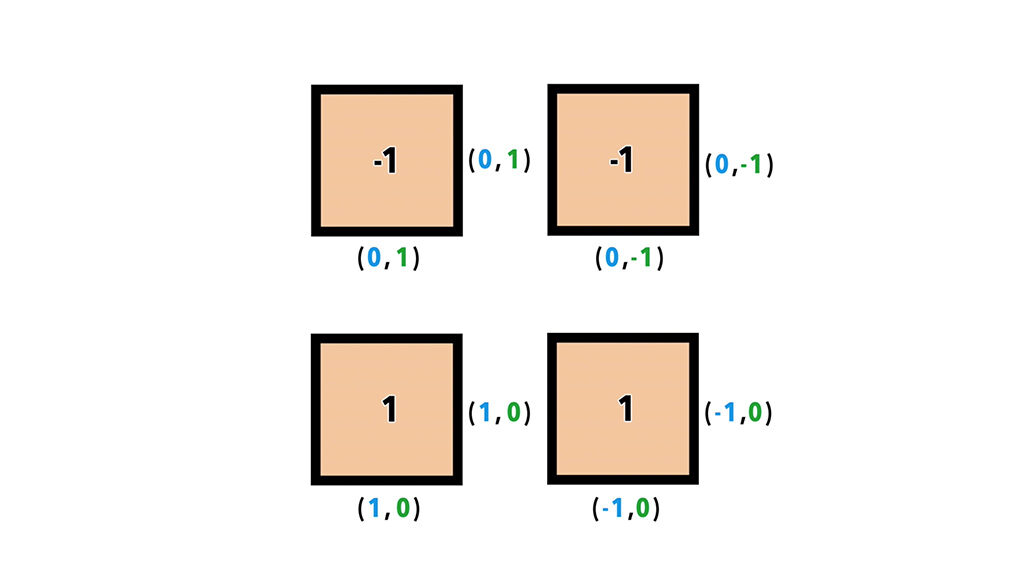
De esta manera si podemos ver que el área negativa de un cuadrado, puede tener 2 lados iguales, porque en 2 dimensiones 2 lados son 4 combinaciones y no 2.
Pero si eres de los que se plantean todo, entiendo te puedas estar confuso o molesto con los números imaginarios, porque ¿qué sentido tiene definir unas reglas para dar una solución que no “existe”? ¿Para qué sirve una solución que no es real? Si te planteas todo esto no te preocupes porque no eres la única persona que se ha hecho esa pregunta.
8.Historia de Números Complejos
En el siglo XV el matemático Rafael Bombelli intentaba resolver una ecuación de tercer grado x³=15x+4 con la fórmula de Cardano. Pero al aplicarla la solución tenía dos raíces negativas de -121.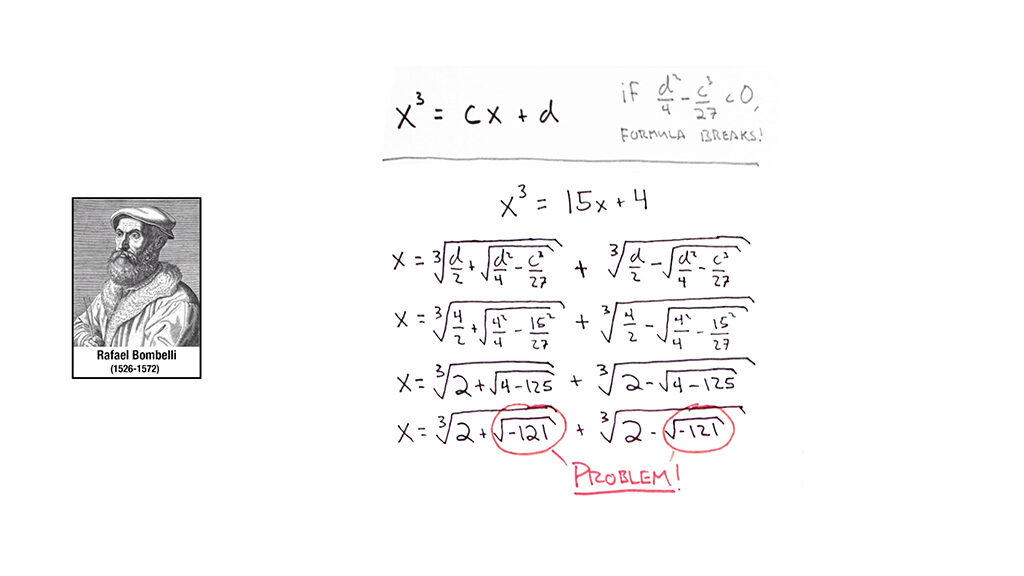 
Como en esa época no se sabía el valor de raiz de -1, Bombelli calculó la solución para la ecuación probando manualmente valores hasta encontrarla. Ahora ya sabía que aunque la expresión tuviera números imaginarios el resultado tenía que ser con seguridad un número real.
Así que se propuso desarrollar la expresión para ver si podía simplificarla, utilizando una de las pocas operaciones complejas que conocía y que era cierta (que la raiz de menos uno al cuadrado tenía que ser -1).
De modo que utilizando la solución que ya conocía y resolviendo un sistema de ecuaciones, pudo simplificar finalmente la fórmula hasta quedarse sin números imaginarios, y obteniendo la solución que esperaba.
Es decir que partiendo de un problema real, calculó una solución real pero operando con números imaginarios, lo cual nos indica que los números imaginarios conectan correctamente ambas dimensiones!!
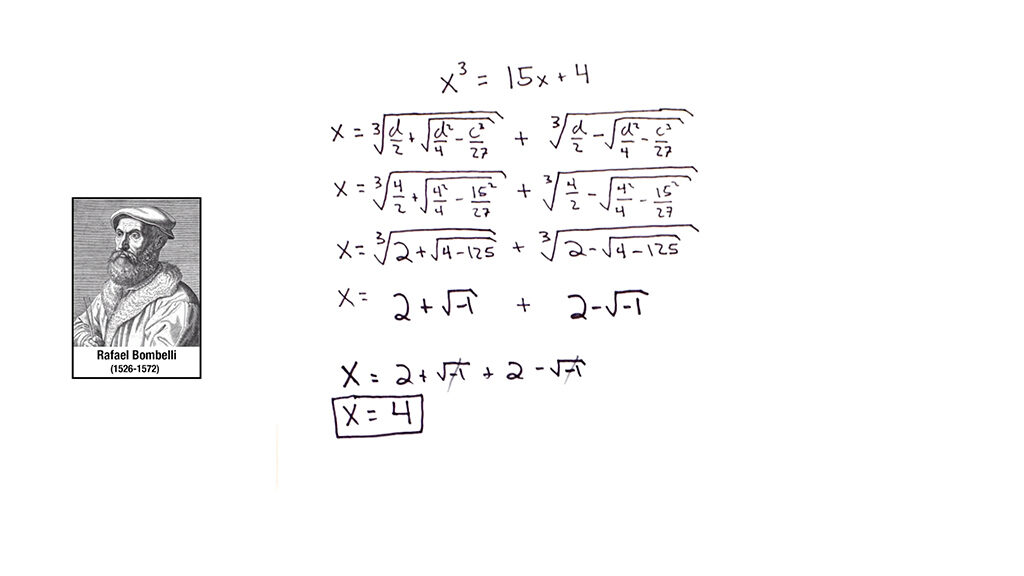
Y en este punto me gustaría pararme y preguntarte: ¿qué es lo real? ¿Acaso los números que conocemos són reales? o pueden considerarse más reales unos que otros? Y en ese caso de ser así, ¿no son más reales aquellos que permiten resolver más problemas, aunque no sean tan intuitivos?
Y es que el error siempre fué llamar real a lo que no es real, e imaginario a lo que no es imaginario. ;). Espero que el video os haya gustado y vuestros comentarios. Y nada esto ha sido todo, así que gracias por vuestro tiempo, y nos vemos en el siguiente video.